Question

Two straight track AOB and COD meet each other at right angles at point O. A person walking at a speed of $5km/h$ along AOB is at the crossing O at 12o’clock noon. Another person walking at the same speed along COD reaches the crossing O at 1:30PM. If the time at which the distance between them is least is 12:T PM, then find T.

Answer 1

The distance can be found by taking the product of speed and the time taken. Also consider the velocity of both the people so that the speed of them will be equal. As asked above to find the time do make the diagram of the condition mentioned above.

Complete step by step solution:

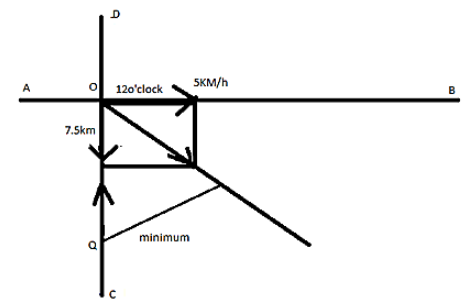
As mentioned above there are two straight tracks so we have taken two tracks AOB and COD they meet at right angles as mentioned above in the diagram. A person crosses AOB at 12 o’clock and the point where two tracks meet is point O and the other person is crossing point at $1:30pm$ .

Let us suppose that the particle is moves in path COD, consider a point Q in the line CO where the another particle starts to move with the speed of $5km/h$ , and the distance between P and Q is,
$dist.= 1.5\times 5=7.5$ ---- (1)

And it is asked in the question that when the separation between them is minimum, so we now we are talking with respect to Q and its velocity is 5km/h and is taken in rest and the velocity of Q is applied on O that is 5km/h. Now the net velocity of P with respect to Q is $5\sqrt{2}$

Now we draw a perpendicular on the track drawn from point O and the line is minimum distance but in question it is not asked that what is the minimum distance they asked the time, so when the person is travelling from point O and the point O shifts to the perpendicular drawn point and the angle is ${{45}^{0}}$.

Now as we know that,
$time=\dfrac{dist.}{velocity}$ ------- (2)
$time= \dfrac{7.5}{5 \sqrt{2}}=\dfrac{3}{4} hour$ ------- (3)

Now on converting equation (3) in minutes,
$time= \dfrac{3}{4} times 60=45\min .$

And hence the required time is $12:45pm$.

Note:
There are so many methods to find the distance from the perpendicular which we drew above in our solution. But the way we find is the standard method to find, that we put one particle in rest and then put the other person in reverse direction and make the path on the line drawn through point O.