Question

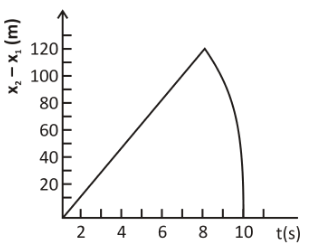
Two stones are thrown up simultaneously from the edge of a cliff $200\,m$ high with initial speeds of $15\,m{s^{ - 1}}$ and $30\,m{s^{ - 1}}$ . Verify that the graph shown in fig. Correctly represents the time variation of the relative position of the second stone with the respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take $g = 10\,m{s^{ - 2}}$ . Give the equations for the linear and curved parts of the plot.

Answer 1

Here we have to first find the time for the first stone and then the second stone using the second equation of motion. With the help of this we can find the maximum separation between the stones. In physics, equations of motion are classified as equations that characterise a physical system’s behaviour in terms of its motion as a function of time. For deriving components such as displacement, velocity, time and acceleration, there are three motion equations that can be used. The first equation of motion deals with acceleration, initial velocity and time.

Complete step by step answer:
For the first stone it is given that:
Initial velocity, ${u_1} = 15m{s^{ - 1}}$
Acceleration,$a = - g = - 10\,m{s^{ - 2}}$
Using the modified form of second equation of motion we get:
${m_1} = {m_ \circ } + {u_1}t + \dfrac{1}{2}a{t^2}$
Here, ${m_ \circ } = 200\,m$

${m_1} = 200 + 15t - 5{t^2}$ ........ (i)
When the stone hits the ground, ${m_1} = 0$
Therefore,$- 5{t^2} + 15t + 200 = 0$
On solving the quadratic equation we get:
$t = 8\,s$ or $t = - 5\,s$
Not considering the negative sign we get:
$t = 8\,s$

For the second stone it is given that:
Initial velocity,${u_1} = 30\,m{s^{ - 1}}$
Acceleration,$a = - g = - 10\,m{s^{ - 2}}$
Using the modified form of second equation of motion we get:
${m_2} = {m_ \circ } + {u_2}t + \dfrac{1}{2}a{t^2}$
Here, ${m_ \circ } = 200\,m$
${m_2} = 200 + 30t - 5{t^2}$ ........ (ii)
When the stone hits the ground, ${m_2} = 0$
Therefore, $- 5{t^2} + 30t + 200 = 0$
On solving the quadratic equation we get:
$t = 10\,s$ or $t = - 4\,s$
Not considering the negative sign we get:
$t = 10\,s$

Subtracting equation (i) from equation (ii) we get:
${m_2} - {m_1} = \left( {200 + 30t - 5{t^2}} \right) - \left( {200 + 15t - 5{t^2}} \right)$
$\Rightarrow {m_2} - {m_1} = 15t$ .......... (iii)
Which is a linear equation.

From this we can gather that the path remains a straight line till $t = 8\,s$ .
So,
${\left( {{x_2} - {x_1}} \right)_{\max }} = 15 \times 8 = 120\,m$
Which is related to the given graph.
After $t = 8\,s$ only second stone is in motion which is given by the quadratic equation:
${m_2} - {m_1} = 200 + 30t - 5{t^2}$
Hence the curved path equation is given by:
${m_2} - {m_1} = 200 + 30t - 5{t^2}$
The equation for the linear path is given by:
${m_2} - {m_1} = 15t$

The equation for the linear path is given as ${m_2} - {m_1} = 15t$ and curved path as ${m_2} - {m_1} = 200 + 30t - 5{t^2}$.

Additional information:
Acceleration is known to be used as a term for speeding up and deceleration for speeding down. However, speeding up may be referred to as positive acceleration and slowing down as negative acceleration.

The average velocity of the object is the total displacement of the object divided by the total time taken. In other words, the pace at which an object changes its location from one place to another. Average velocity is a quantity of vectors. The SI unit is one metre per second.

Note: Here we have to see that the initial velocity varies for both the stones. Also, we have to be careful while calculating the quadratic equation. We cannot consider the value with the negative sign.The sum of the original and final velocity is separated by $2$ in order to find the average. The average velocity calculator uses a formula that indicates the average velocity equal to the sum of the final velocity and the original velocity over $2$.