Question
Question: . Two stones are thrown up simultaneously from the edge of a cliff \(240m\) high with initial speed ...
. Two stones are thrown up simultaneously from the edge of a cliff 240m high with initial speed of 10m/s and 40m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? (Assume stones do not rebound after hitting the ground and neglect air resistance, take (g=10m/s2)
(a)
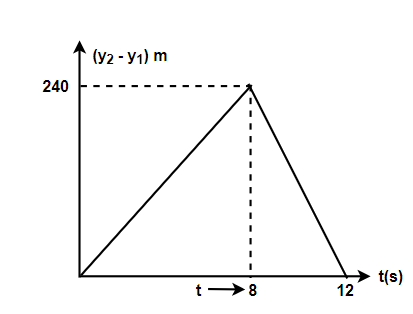
(b)
(c)
(d)
Solution
Hint The concept of relative motion can be applied to predict the nature of motion of one particle with respect to the other stones do not rebound after hitting the ground and neglect air resistance,
Complete step by step solution:
Consider the stones thrown up simultaneously as shown in diagram below
Considering the motion of second particle with respect to the first we have relative acceleration
⇒a21=a2−a1=g−g=0
Thus, the motion of the first particle is straight line with respect to the second particle till the first particle strikes ground at a time given by
⇒−240=10t−21×10×t2
On solving it, we get
⇒t2−2t−48=0
And it can be written as
⇒t2−8t+6t−48=0
Solving it, we get
⇒t2=8,−6
−6 is not possible because it is in negative
Thus, distance covered by the second particle with respect to the first particle in 8sis
S12=(V21)t
Vbe velocity Now substitute the values
⇒S12=(40−10)8
And on solving it, we get the value as
⇒S12=30×8=240m
Similarly, time taken by the second particle to strike the ground is given by
⇒−240=40t−21×10×t2
And on solving the RHS, we get
⇒−240=40t−5t2
It can be written as
⇒5t2−40t−240=0
Taking common, we get the equation as
⇒t2−8t−48=0
Solving it,
⇒t2−12t+4t−48=0
We get the factor as
⇒t(t−12)+4(t−12)=0
After solving equation we got the values
⇒t=12,−4
−4 is not possible because it is in negative
Hence we take t=12s
Thus after 8s the magnitude of relative velocity will increase up to 12s when the second particle strike the ground
Hence the correct option is (a)
Note: Relative velocity is the vector difference between the velocities of two bodies: the velocity of a body with respect to another regarded as being at rest. So we had selected the correct option according to the obtained result.
