Question
Question: Two square plates \( l \times l \) and dielectric \( \left( {\dfrac{l}{2} \times \dfrac{t}{2} \times...
Two square plates l×l and dielectric (2l×2t×l) are arranged in figure. Find the equivalent capacitance of the structure.
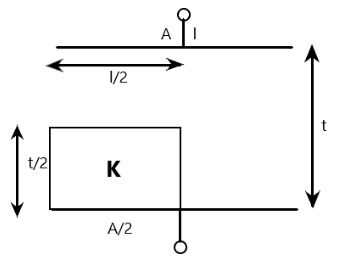
(A) tε0A(2(K+1)3K+1)
(B) t2ε0A((K+3)K+1)
(C) tε0A((K+3)K+1)
(D) tε0A(2K+32K+1)
Solution
The system acts like three capacitors in general. The capacitor with the dielectric, the capacitor without the dielectric (which ends where the dielectric ends) just above the dielectric, and the capacitor right of them both. The dielectric capacitor and the capacitor above it are in series, and the one on the right is in parallel to them.
Formula used: In this solution we will be using the following formulae;
C=dεoA where C is the capacitance of a capacitor without a dielectric, εo is the permittivity of free space, A is the area of the plate of the capacitor and d is the separation.
Cd=dKεoA where Cd is the capacitance of a capacitor with dielectric, and K is the dielectric constant of the dielectric.
Ceqs1=C11+C21 where Ceqs is the effective capacitance of two capacitors in series, C1 and C2 are the individual capacitance of series capacitors.
Ceqp=C1+C2 where Ceqp is the equivalent capacitance of two capacitors in parallel, and C1 and C2 are the individual capacitors in parallel.
Complete Step-by-Step solution:
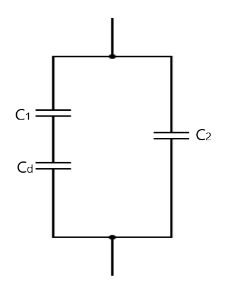
To answer this, we note that the dielectric will act as a capacitor which is in series to a capacitor of free space above it, as seen in the diagram above.
The capacitance of a capacitor with dielectric can be given as
Cd=dKεoA where K is the dielectric constant of the dielectric, εo is the permittivity of free space, A is the area of the plate of the capacitor and d is the separation.
For this dielectric, as seen from question, it would be
Cd=2tKεo2A=tKε0A
Capacitors without dielectric is given by
C=dεoA
Hence, for the capacitor C1 , we have
C1=2tεo2A=tε0A
The equivalent capacitance of capacitors in series is given as
Ceqs1=C11+C21 where C1 and C2 are the individual capacitance of series capacitors.
Hence, for Cd and C1 , we have
Ceqs1=ε0At+Kε0At=Kε0At(K+1)
⇒Ceqs=t(K+1)Kε0A
This capacitor is now in parallel with the capacitor C2
C2 can be given as
C2=tεo2A=2tε0A
Capacitors in parallel is given as
Ceqp=C1+C2 where C1 and C2 are the individual capacitors in parallel.
Hence,
Ceqv=Ceqs+C2=t(K+1)Kε0A+2tε0A
Hence, we have
⇒Ceqv=2t(K+1)2Kε0A+Kε0A+ε0A=tε0A(2(K+1)3K+1)
Hence, the correct option is A.
Note:
For clarity, even though the dielectric does not have a plate, to cover it as a normal capacitor, it still behaves as a normal capacitor. This is because capacitors in series, for example, only one of the plates of one capacitor will be connected to the voltage source. Hence, without unconnected plates, the capacitors behave just the same.
