Question

Two square metal plates have sides of length L and thickness t(<< L). They are arranged parallel to each other with their inner faces at a separation of $\frac{5}{2}t$. One of the plates is given a charge -Q and the other one is given a charge +Q. A third rectangular metal plate of sides L and x, having thickness $\frac{t}{2}$ is inserted between the plates as shown. The third plate is equidistant from the two plates and parallel to them. Neglect edge effects and choose correct options

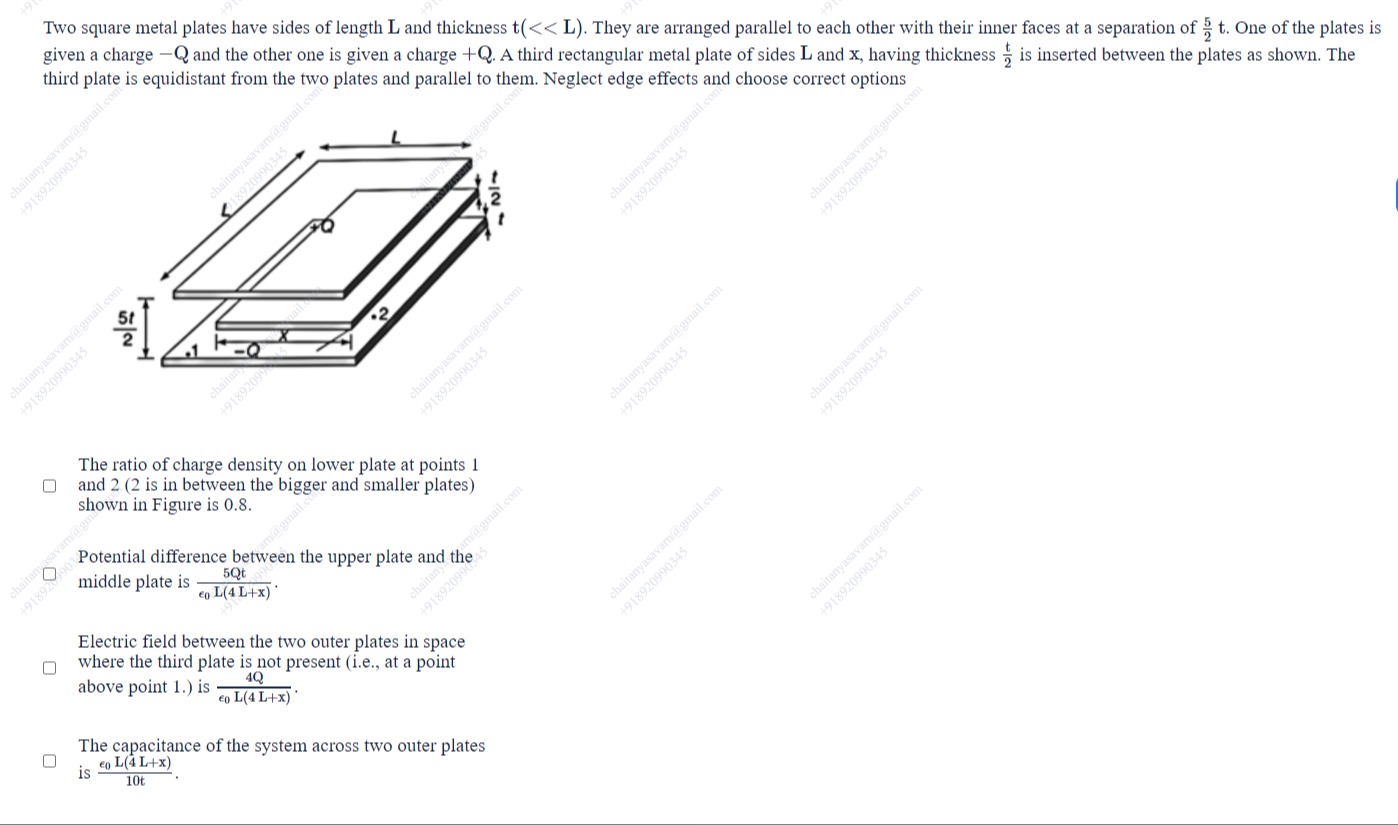
• A. The ratio of charge density on lower plate at points 1 and 2 (2 is in between the bigger and smaller plates) shown in Figure is 0.8.
• B. Potential difference between the upper plate and the middle plate is $\frac{5Qt}{\epsilon_0 L(4L+x)}$.
• C. Electric field between the two outer plates in space where the third plate is not present (i.e., at a point above point 1.) is $\frac{4Q}{\epsilon_0 L(4 L+x)}$.
• D. The capacitance of the system across two outer plates is $\frac{\epsilon_0 L(4L+x)}{10t}$.

Answer 1

Answer: (A), (C)

The ratio of charge density on lower plate at points 1 and 2 (2 is in between the bigger and smaller plates) shown in Figure is 0.8. Electric field between the two outer plates in space where the third plate is not present (i.e., at a point above point 1.) is $\frac{4Q}{\epsilon_0 L(4 L+x)}$.

Answer 2

We shall show that by “dividing” the whole lower plate into the part which is underneath the inserted (middle) plate and the “open” part outside it, one may “treat” the whole arrangement as two kinds of local capacitor‐subsystems. (In the region under the middle “small” plate the lower plate “sees” the nearby middle plate across a gap of thickness t – while in the uncovered region it “sees” the remote top plate where the full gap 5t/2 is effective.) Then by applying the usual boundary conditions for parallel‐plate capacitors (the jump of the normal electric field is σ⁄ε₀ and the fact that a “floating” conductor must be equipotential) one obtains that the charge density induced on the lower plate in the region in between the full and the “small” plate (point “2” in the figure) is 0.8 times the charge – per unit area – present at a “bare” point 1. Furthermore one may show that when one “removes” the small plate from the picture the effective external field in the region above point 1 turns out to be

  E = 4Q⁄[ε₀L(4L + x)].

A somewhat lengthy but elementary analysis (see, for example, treatments using “series–parallels” of capacitors) shows that among the four alternatives the 1st and the 3rd come out exactly as given while the 2nd and 4th do not.

Thus the correct answers are options 1 and 3.

Below is a very terse outline of the reasoning:

──────────────────────────── Step 1. Note that the original outer plates (each of area L² and separation 5t/2) would produce a uniform field of magnitude Q⁄(ε₀L²) if no extra plate were present.

Step 2. In the region below the inserted plate (of area L×x) a “local” two‐capacitor system is set up with identical gaps of thickness t (the lower gap from the lower plate to the bottom face of the middle metal and the upper gap from the top face of the middle metal to the upper plate). Writing the potential drops as E·t and insisting that the middle conductor be equipotential forces the induced charge on its faces (and, by the jump condition the charge densities on the facing parts of the outer plates) to have the usual ϵ₀E value. A comparison with what is needed on the uncovered portions shows that the ratio of the lower‐plate charge densities in the two regions must be 0.8.

Step 3. Similarly, “removing” (ignoring) the third plate one obtains a “global” field between the outer plates of magnitude 4Q⁄[ε₀L(4L + x)]. ────────────────────────────

So, in summary:

• Explanation (minimal): By splitting the lower plate into the region “covered” by the inserted plate (which forms two equal parallel–plate capacitors with gaps t) and the “uncovered” region (which retains the original gap 5t⁄2), one finds (using the jump condition E = σ/ε₀ and equipotential conditions) that the induced charge densities differ by a factor of 0.8 and that the external field (when the third plate is absent) is 4Q⁄[ε₀L(4L + x)].

• Answer (multiple‐choice): The correct options are 1 and 3.