Question
Question: Two springs are connected in series and the combination is pulled by a constant force. If spring con...
Two springs are connected in series and the combination is pulled by a constant force. If spring constant of two springs are K\text{ and 2}K$ , then the ratio of potential energy stored in the springs is
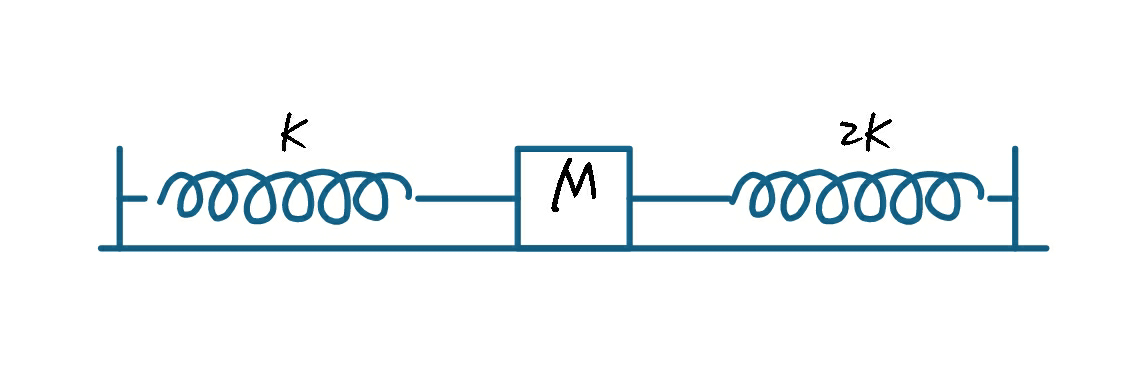
Solution
Hint We know that PE is the amount of energy started at the highest point.
Here, two springs are converted in series
Therefore, using P.E=21K2
Complete Step by Step Solution
2:1
For spring S1 the spring constant is K
For springS2 the spring constant is 2K
Now, applying the potential energy formula for spring S1
i.e. PE1=21Kr2 …… (1)
Similarly, we use the above formula for spring S2
i.e.PE2=212K x2 …… (2)
Now, dividing equation (2) by equation (1)
We get PE1PE2=21Kx2×(2K)x22
Now, cancelling all the common factors in the above equation we get
PE1PE2=21
Or for simplicity we can write this as also
PE1PE2=21
Therefore, the ratio of the two potential angles is 2:1
Note Above discussion of Potential Energy that is stored in the spring can be found out using 21kx2formula in whichk=Spring Constant.
In this case, we reciprocate this energy with respect to the other.
