Question
Question: Two spherical conductors \[{A_1}\] and \[{A_2}\] of radii \[{r_1}\] and \[{r_2}\]\[\left( {{r_2} > {...
Two spherical conductors A1 and A2 of radii r1 and {r_2}$$$$\left( {{r_2} > {r_1}} \right)are placed concentrically in air. A1is given a charge +Q while A2 is earthed. Then the equivalent capacitance of the system is:
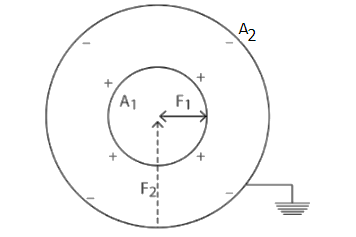
A. r2−r14πε0r1r2
B. 4πε0(r1+r2)
C. 4πε0r2
D. 4πε0r1
Solution
Formula for capacitance is given by, C=VQ. Here, Q is the charge. Apply Gauss’s law to obtain the value of the electric field E in terms of VQ.
Complete step by step solution:
Given, the radii of the conductors A1and A2 are r1and r2 respectively.
Here, r2>r1
By Gauss's law the electric field at a point r in between the shells is given by,
E4πr2=ε0Q
Rearrange the above equation in terms of electric field E.
E=4πr2ε0Q
Now, the potential difference between the shells is given by,
∫0VdV=−∫r2r1Edr
Place the value of E=4πr2ε0Q in the above equation and simplify.
\int_0^V {dV} = - \int_{{r_2}}^{{r_1}} {\dfrac{Q}{{4\pi {r^2}{\varepsilon _0}}}dr} \\\ V = - \dfrac{Q}{{4\pi {\varepsilon _0}}}\int_{{r_2}}^{{r_1}} {\dfrac{{dr}}{{{r^2}}}} \\\ V = - \dfrac{Q}{{4\pi {\varepsilon _0}}}\left( {\dfrac{1}{{{r_2}}} - \dfrac{1}{{{r_1}}}} \right) \\\ V = \dfrac{Q}{{4\pi {\varepsilon _0}}}\left( {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right) \\\ V = \dfrac{Q}{{4\pi {\varepsilon _0}}}\dfrac{{{r_2} - {r_1}}}{{{r_1}{r_2}}} \\\ $$ …… (i) Capacitance is the ratio of a system's change in electrical charge and the resulting change in its electrical potential. The formula for capacitance is given by, $$C = \dfrac{Q}{V}$$ …… (ii) Rearrange the equation (i) in terms of $$\dfrac{Q}{V}$$ and we get, $$\dfrac{Q}{V} = \dfrac{{4\pi {\varepsilon _0} \times {r_1}{r_2}}}{{{r_2} - {r_1}}}$$ Place the above value in equation (ii) $$C = \dfrac{{4\pi {\varepsilon _0}{r_1}{r_2}}}{{{r_2} - {r_1}}}$$ **Hence, the correct answer is option A.** **Additional information:** Gauss’s law: The electrical flux sum of a closed surface is equal to the enclosed charge separated by permittivity. The electric flux through a region is known as the electric field multiplied in a plane perpendicular to the field by the area of the surface predicted. Simply put, Gauss' law states that the overall electric charge within a container can be determined by measuring the net electric field flux flowing out of a sealed surface covering the volume. **Note:** In this question we are asked to determine the value of capacitance which is given by, $$C = \dfrac{Q}{V}$$. The electrical flux sum of a closed surface is equal to the enclosed charge separated by permittivity. i.e. $$E4\pi {r^2} = \dfrac{Q}{{{\varepsilon _0}}}$$. The potential difference between the shells is given by, $$\int_0^V {dV} = - \int_{{r_2}}^{{r_1}} {Edr} $$. Solve the equation in terms of $$\dfrac{Q}{V}$$.