Question

Two spherical bodies of masses M and 5M and radii R and 2R respectively are released in free space with the initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then find the distance covered by the smaller body just before the collision.

Answer 1

Hint: Consider a point where these two bodies of mass M and 2M are going to meet. And mark that distance from these two bodies. The gravitational force acting on each body will be the same, taking help of this to find the relation between these marked distances with the given distance 12R.

Complete step by step solution:
Let us draw the diagram of the above question.

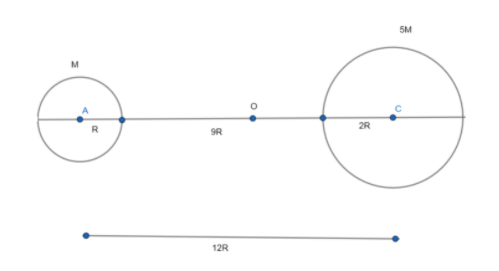
Formula Used:
Gravitational Force between two objects of mass M and m separated by distance r is given by
$F=\dfrac{GMm}{{{r}^{2}}}$
Complete step by step answer:
Let us first understand the Gravitational Force
Gravitational Force: When two bodies that are placed in rest are started to attract each other, this attractive force is called gravitational force. This force is directly proportional to the product of masses of two objects and inversely proportional to square of the distance separating them.
$F=\dfrac{GMm}{{{r}^{2}}}$
Where:
G = Gravitational Constant which has the value of $6.67\times {{10}^{-11}}{{m}^{3}}{{s}^{-2}}k{{g}^{-2}}$
M and m are the masses of two objects
r = distance of separation of two objects.
In our question force acting by each of the body on one another is same i.e. $F=\dfrac{5G{{M}^{2}}}{{{\left( 12R \right)}^{2}}}$. Also force is equal to mass time acceleration.
$F=ma$
Here, force is constant therefore, acceleration is inversely proportional to mass.
$a\propto \dfrac{1}{m}$
Acceleration due to mass 5M
${{a}_{5M}}\propto \dfrac{1}{5M}$
Acceleration due to mass M
${{a}_{M}}\propto \dfrac{1}{M}$
Comparing acceleration we get:
$\begin{aligned} & \\\ & \dfrac{{{a}_{5M}}}{{{a}_{M}}}=\dfrac{M}{5M} \\\ & \dfrac{{{a}_{5M}}}{{{a}_{M}}}=\dfrac{1}{5} \\\ \end{aligned}$
Initially both the bodies are at rest (i.e. u=0), therefore by applying third equation of motion $s=ut+\dfrac{1}{2}a{{t}^{2}}$
Small body will travel distance ${{x}_{M}}$ and big body will travel ${{x}_{5M}}$ distance to collide in the same time i.e. $t$
${{x}_{M}}=\dfrac{1}{2}{{a}_{M}}{{t}^{2}}$ and ${{x}_{5M}}=\dfrac{1}{2}{{a}_{5M}}{{t}^{2}}$. After dividing these two equation
$\begin{aligned} & \dfrac{{{x}_{5M}}}{{{x}_{M}}}=\dfrac{{{a}_{5M}}}{{{a}_{M}}} \\\ & \dfrac{{{x}_{5M}}}{{{x}_{M}}}=\dfrac{1}{5} \\\ & {{x}_{M}}=5{{x}_{5M}} \\\ \end{aligned}$
In the diagram it is clear that ${{x}_{M}}+{{x}_{5M}}=9R$
And,
$\begin{aligned} & 5{{x}_{5M}}+{{x}_{5M}}=9R \\\ & 6{{x}_{5M}}=9R \\\ & {{x}_{5M}}=1.5R \\\ & \therefore {{x}_{M}}=7.5R \\\ \end{aligned}$
Therefore, the distance travelled by a small body just before collision is 7.5R.

Note: Sometimes students may make mistakes while putting the distance directly from the centre to the point where bodies are going to collide. But remember to subtract their radius to the distance of the line joining two bodies. By this way you will get the correct answer.