Question

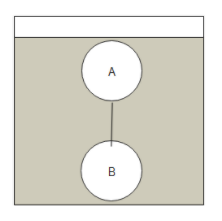
Two solid spheres A and B of equal volumes but of different densities ${d_A}$ and ${d_B}$ are connected by a string. They are fully immersed in a fluid of density ${d_F}$ ​. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if:
A.\eqalign{ & {d_A} > {d_F} \cr}
B.\eqalign{ & {d_B} > {d_F} \cr}
C.\eqalign{ & {d_A} < {d_F} \cr}
D.\eqalign{ & {d_A} + {d_B} = 2{d_F} \cr}

Answer 1

In this question, we will use the relation between the densities, volumes and gravity of the two spheres at top and bottom. Further, we will deduce the required relation between the densities of the two spheres. Also, we will study some basics of the principle that comes into action when an object is placed or immersed in fluid.
Formula used-
\eqalign{ & V{d_F}g = T + V{d_A}g \cr & T + V{d_F}g = V{d_B}g \cr}

Complete answer:
For sphere A to be on the top in liquid, the density of sphere A should be less than the density of the liquid. Also, for sphere B to be at the bottom of the given liquid, the density of sphere B should be greater than the density of the liquid.
So, we get the relation for the top and the bottom sphere as:
\eqalign{ & V{d_F}g = T + V{d_A}g \cr & T + V{d_F}g = V{d_B}g \cr}
Substituting the value of T will give us:
\eqalign{ & 2V{d_F}g = V{d_A}g + V{d_B}g \cr & \therefore 2{d_F} = {d_A} + {d_B} \cr}

Therefore, from this result we can say option D) is correct i.e., the arrangement of the two spheres to be in an equilibrium state is given by the above relation.

Additional information:
Archimedes principle states that an object immersed in a fluid experiences some buoyant force that is equal in magnitude to the force of gravity on the displaced fluid. It is also known as the law of buoyancy.
The weight of the displaced fluid is equal to the subtraction of weight of object in vacuum and weight of object in fluid. This principle was discovered by the ancient Greek mathematician and inventor Archimedes.
We should also know about the buoyant force. This is an upward force exerted by a fluid which opposes the weight of a partially or fully immersed object in the fluid. Here, in the fluid, pressure increases with depth as a result of the weight of the overlying fluid. So, the pressure at the bottom of a column of fluid is greater than at the top of the column.

Note:
One should notice that the Archimedes principle is only valid for fluids, where buoyant force can be observed. Also, the displaced fluid is equal to the weight of the object immersed in the water. In the displaced fluid, gravity also plays an important role.