Question

Two solenoids of an equal number of turns having their length and radii in the same ratio 1:2. The ratio of their self-inductance will be:
A) 1:2
B) 2:1
C) 1:1
D) 1:4

Answer 1

Here we have given two solenoids whose number of turns are the same and the length and the radii of both the solenoids are in ratio 1:2. We have to find the ratio of self-inductance for these two solenoids. Hence by using the formula of self-inductance we can find the ratio. We can also draw a simple diagram for better understanding.
Formula used:
$L=\dfrac{{{\mu }_{0}}{{N}^{2}}A}{l}$

Complete step-by-step solution
Let us first draw a simple diagram for the given question.

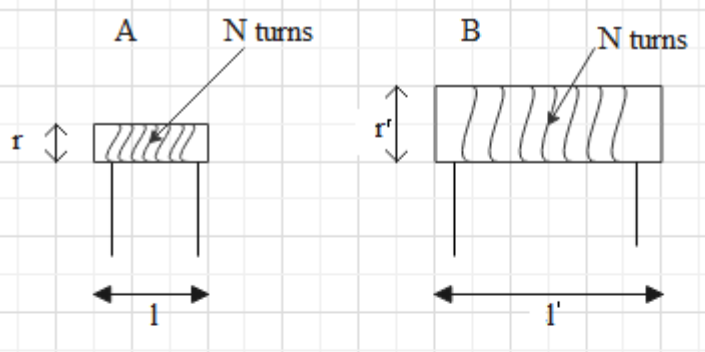
As we can see there are two solenoids A and B. The number of turns of both solenoids is the same. The length of A is l and the length of B is l’. Similarly, the radius of A is r, and the radius of B is r’.
Now we know that self-inductance is a property of a coil by which it opposes the change in the current flowing through it and generates an induced emf. Self-inductance of a solenoid is directly proportional to the number of turns and cross-sectional areas whereas it is inversely proportional to the length. Therefore, its formula can be given as
$L=\dfrac{{{\mu }_{0}}{{N}^{2}}A}{l}$
Here A is the cross-sectional area, N is the number of turns, l is the length and ${{\mu }_{0}}$is the permeability in free space.
We know the cross-sectional area of solenoid is given as $4\pi {{r}^{2}}$, substituting this value in above equation, we get
$L=\dfrac{4\pi {{\mu }_{0}}{{N}^{2}}{{r}^{2}}}{l}$
So self-inductance for solenoid A can be given by above formula, if number of turns for A is N. Where for solenoid B having same number of turns i.e. N, self-inductance can be given as
$L'=\dfrac{4\pi {{\mu }_{0}}{{N}^{2}}r{{'}^{2}}}{l'}$
Now the ration of self-inductance of A to B can be given as

& \dfrac{L}{L'}=\dfrac{\dfrac{4\pi {{\mu }_{0}}{{N}^{2}}{{r}^{2}}}{l}}{\dfrac{4\pi {{\mu }_{0}}{{N}^{2}}r{{'}^{2}}}{l'}} \\\ & \Rightarrow \dfrac{L}{L'}=\dfrac{{{r}^{2}}l'}{r{{'}^{2}}l} \\\ & \Rightarrow \dfrac{L}{L'}={{\left( \dfrac{r}{r'} \right)}^{2}}\left( \dfrac{l'}{l} \right)\text{ }...........\text{(i)} \\\ \end{aligned}$$ Now according to the question, the ratio of length and radius of solenoid A and B is given as $$\begin{aligned} & \dfrac{l}{l'}=\dfrac{1}{2} \\\ &\Rightarrow \dfrac{r}{r'}=\dfrac{1}{2} \\\ \end{aligned}$$ Now substituting value of ratio of length and radius in equation (i), we get $$\begin{aligned} & \dfrac{L}{L'}={{\left( \dfrac{1}{2} \right)}^{2}}\left( \dfrac{2}{1} \right) \\\ & \Rightarrow \dfrac{L}{L'}=\left( \dfrac{1}{4} \right)\left( 2 \right) \\\ & \Rightarrow \dfrac{L}{L'}=\dfrac{1}{2} \\\ \end{aligned}$$ **Hence the ratio of self-inductance is 1:2. So, Option A is correct.** **Note:** We didn’t use different symbols for the number of turns for A and B because it has the same values. Self-inductance is associated with a single coil or solenoid, when two coils are placed then it will also have mutual inductance. Mutual inductance is basically the induced emf in one coil due to a change in current or change in flux in another coil.