Question

Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure $8N/{{m}^{2}}$. The radii of bubble A and B are 2 cm and 4 cm, respectively. Surface tension of the soap water used to make bubbles is 0.04 N/m. Find the ratio $\dfrac{nB}{nA}$, where $nA$ and $nB$ are the number of moles of air in bubbles A and B, respectively. (Neglect the effect of gravity).

Answer 1

We are given the radii of two soap bubbles, the surface tension of the soap water used to make the bubbles and the pressure of the chamber where these bubbles are kept. By finding the pressure and volume of these two bubbles and substituting it in the ideal gas equation and then taking the ratio of these two equations we will get the required ratio.
Formula used:
$P={{P}_{0}}+\dfrac{4T}{r}$
$V=\dfrac{4}{3}\pi {{r}^{3}}$
$PV=nRT$

Complete answer:
In the question we are given two soap bubbles ‘A’ and ‘B’ which are placed in a closed chamber.
The pressure of the air in the chamber is $8N/{{m}^{2}}$. This is the external pressure, i.e.
${{P}_{0}}=8N/{{m}^{2}}$
Surface tension of the soap water used to make the two soap bubbles is given as 0.04 N/m, i.e.
$T=0.04N/m$
Now let us consider the soap bubble ‘A’.
Let ‘${{r}_{A}}$’ be the radius of the soap bubble ‘A’, then we are given,
${{r}_{A}}=2cm=2\times {{10}^{-2}}m$
Let ‘${{P}_{A}}$’ be the pressure inside the soap bubble ‘A’.
We know that pressure inside is a bubble is given by the equation,
$P={{P}_{0}}+\dfrac{4T}{r}$, were ‘P’ is the inside pressure, ‘${{P}_{0}}$’ is the outside pressure, ‘T’ is the surface tension and ‘r’ is the radius of the bubble.
Therefore the pressure inside the soap bubble ‘A’ is,
$\Rightarrow {{P}_{A}}={{P}_{0}}+\dfrac{4T}{{{r}_{A}}}$
By substituting for the known values in the above equation,
$\Rightarrow {{P}_{A}}=8+\dfrac{4\times 0.04}{2\times {{10}^{-2}}}$
By solving this we get,
$\Rightarrow {{P}_{A}}=16N/{{m}^{2}}$
Now we can calculate the volume of the soap bubble ‘A’.
The equation for volume of sphere is,
$V=\dfrac{4}{3}\pi {{r}^{3}}$
Since soap bubble is sphere, the volume of soap bubble ‘A’ will be,
${{V}_{A}}=\dfrac{4}{3}\pi {{r}_{A}}^{3}$
By substituting for radius of the bubble ‘A’,
$\Rightarrow {{V}_{A}}=\dfrac{4}{3}\pi \times {{\left( 2\times {{10}^{-2}} \right)}^{3}}$
From the ideal gas equation, we know that
$PV=nRT$
Now let us find the ideal gas equation of the soap bubble ‘A’. it will be,
${{P}_{A}}{{V}_{A}}={{n}_{A}}RT$
By substituting for pressure and volume, we get
$\Rightarrow \left( 16 \right)\left( \dfrac{4}{3}\pi \times {{\left( 2\times {{10}^{-2}} \right)}^{3}} \right)={{n}_{A}}RT$
This is the ideal gas equation of soap bubble ‘A’.
Now let us consider the soap bubble ‘B’.
Let ‘${{r}_{B}}$’ be the radius of the bubble ‘B’. We are given,
${{r}_{B}}=4cm=4\times {{10}^{-2}}m$
Let ‘${{P}_{B}}$’ be the pressure inside the bubble ‘B’, then we know that,
${{P}_{B}}={{P}_{0}}+\dfrac{4T}{{{r}_{B}}}$
By substituting for the known values, we get
$\Rightarrow {{P}_{B}}=8+\dfrac{4\times 0.04}{4\times {{10}^{-2}}}$
By solving this we get,
$\Rightarrow {{P}_{B}}=12N/{{m}^{2}}$
Now let us find the volume of the soap bubble ‘B’.
We know that,
${{V}_{B}}=\dfrac{4}{3}\pi {{r}_{B}}^{3}$
By substituting for radius of the bubble ‘B’, we get
$\Rightarrow {{V}_{B}}=\dfrac{4}{3}\pi {{\left( 4\times {{10}^{-2}} \right)}^{3}}$
Now we know that the ideal gas equation for the soap bubble ‘B’ is given as,
${{P}_{B}}{{V}_{B}}={{n}_{B}}RT$
By substituting for pressure and volume of the bubble ‘B’, we get
$\Rightarrow \left( 12 \right)\left( \dfrac{4}{3}\pi {{\left( 4\times {{10}^{-2}} \right)}^{3}} \right)={{n}_{B}}RT$
This is the ideal gas equation for the bubble ‘B’.
In the question we are asked to find the ratio of number of moles of air in bubbles B and A. for that let us divide the ideal gas equation for the bubble ‘A’ by the ideal gas equation for the bubble ‘B’, i.e.
$\dfrac{{{P}_{A}}{{V}_{A}}}{{{P}_{B}}{{V}_{B}}}=\dfrac{{{n}_{A}}RT}{{{n}_{B}}RT}$
$\Rightarrow \dfrac{\left( 16 \right)\left( \dfrac{4}{3}\pi \times {{\left( 2\times {{10}^{-2}} \right)}^{3}} \right)}{\left( 12 \right)\left( \dfrac{4}{3}\pi {{\left( 4\times {{10}^{-2}} \right)}^{3}} \right)}=\dfrac{{{n}_{A}}RT}{{{n}_{B}}RT}$
By eliminating the common terms in the equation, we get
$\Rightarrow \dfrac{\left( 16 \right){{\left( 2\times {{10}^{-2}} \right)}^{3}}}{\left( 12 \right){{\left( 4\times {{10}^{-2}} \right)}^{3}}}=\dfrac{{{n}_{A}}}{{{n}_{B}}}$
By solving this we get the ratio of $\dfrac{nB}{nA}$ as,
$\Rightarrow \dfrac{{{n}_{A}}}{{{n}_{B}}}=\dfrac{1}{6}$
We need to find $\dfrac{{{n}_{B}}}{{{n}_{A}}}$. This is the reciprocal of $\dfrac{{{n}_{A}}}{{{n}_{B}}}$. Therefore,
$\Rightarrow \dfrac{{{n}_{B}}}{{{n}_{A}}}=6$
Hence the ratio of the number of moles of air in bubbles B and A is 6.

Note:
Consider a soap bubble of radius ‘r’ as shown below.

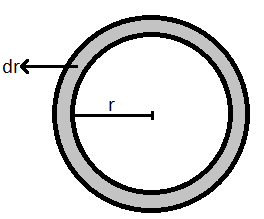
Let ‘$T$’ be the surface tension of the soap bubble.
Let ‘${{P}_{i}}$’ be the pressure inside the bubble and ‘${{P}_{0}}$’ be the pressure outside the bubble.
We know that due to surface tension the surface molecules of the bubble experience a net force inwards and thus the pressure inside the bubble will be greater than the pressure outside.
Then we get the excess pressure inside the bubble will be,
$P={{P}_{i}}-{{P}_{0}}$
Due to this excess pressure, the free surface will expand outwards. Let this expansion be ‘$dr$’
We know that the work done in displacing the excess pressure is stored as the potential energy.
Therefore the small work done,
$dW=P\times A\times dr$, where ‘P’ is the excess pressure, ‘A’ is the surface area and ‘$dr$’ is the displaced surface.
We know that $A=4\pi {{r}^{2}}$
Therefore,
$\Rightarrow dw=P\times 4\pi {{r}^{2}}\times dr$
Then the increase in the potential energy due to the work done,
$dU=TA'$, where ‘T’ is the surface tension and ‘$A'$’ is the increase in the area of the free surface.
We know that $A'=2\left( 4\pi {{\left( r+dr \right)}^{2}}-4\pi {{r}^{2}} \right)$
Therefore,
$\Rightarrow dU=T\times \left( 2\left( 4\pi {{\left( r+dr \right)}^{2}}-4\pi {{r}^{2}} \right) \right)$
$\Rightarrow dU=T\left( 2\left( 4\pi \left( 2rdr \right) \right) \right)$
Since $dw=dU$, we get
$\Rightarrow P\times 4\pi {{r}^{2}}\times dr=T\left( 2\left( 4\pi \left( 2rdr \right) \right) \right)$
$\Rightarrow P\times 4\pi {{r}^{2}}\times dr=T16\pi rdr$
$\Rightarrow P\times r=4T$
$\Rightarrow P=\dfrac{4T}{r}$
Therefore the pressure inside the soap bubble, $P=\dfrac{4T}{r}$