Question
Question: Two smooth cylindrical bars weighing W each lie next to each other in contact. A similar third bar i...
Two smooth cylindrical bars weighing W each lie next to each other in contact. A similar third bar is placed over the two bars as shown in figure. Neglecting friction, the minimum horizontal force on each lower bar necessary to keep them together is-
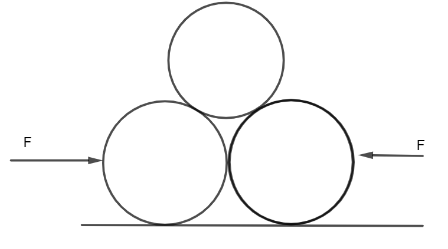
A. 2W
B. W
C. 3W
D. 23W
Solution
Let us first get some idea about force. A force is an external agent capable of altering a body's condition of rest or motion. There is a magnitude and a direction to it. The force's direction is known as the force's direction, and the location where force is applied is known as the point where force is applied.
Complete step by step answer:
The normal force between the lower cylinders must be zero for the system to be in equilibrium, which can be done by applying an external force F as shown in the diagram.Let us get some ideas about free body diagrams. A free body diagram is a diagrammatic representation of a single body or a subsystem of bodies that has been isolated from its surroundings and depicts all of the forces acting on it.
A free body diagram is a graphical image used in physics and engineering to visualise the applied forces, moments, and consequent reactions on a body under a particular condition. They show a body or a group of bodies, as well as all the applied forces, moments, and responses that act on the body (ies).
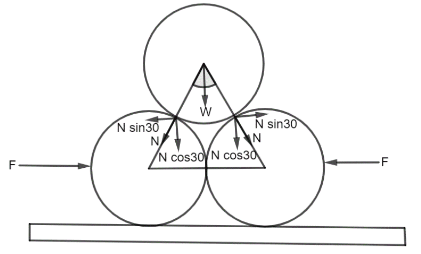
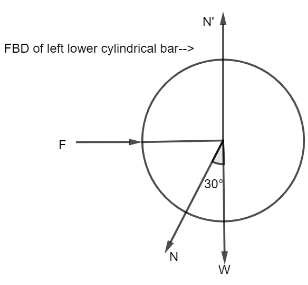
We can write the following on the basis of the free body diagram of the left lower cylindrical bar:
F=Nsin30∘ …(1)
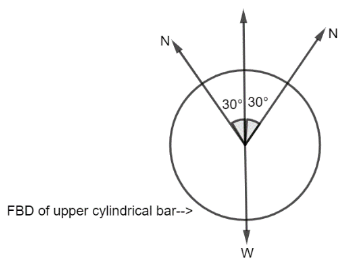
Hence, using the free body diagram of the left lower cylindrical bar as a guide, we may write:
W=2Ncos30∘ ….(2)
Now diving Eq (1)and Eq(2): (2)(1)
WF=2Ncos30∘Nsin30∘
⇒F=2cos30∘Wsin30∘
⇒F=2Wtan30∘
⇒F=2W(31)
∴F=23W
So,option D is correct.
Note: In order to solve this problem there are some very important points which we should keep on our finger tip. Making a free body diagram is very important here and vector resolution and breaking into components is also important for solving this problem.
