Question

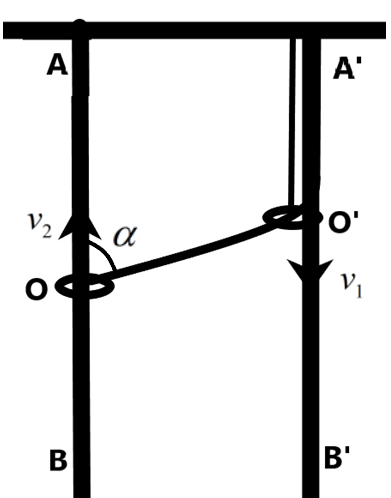
Two small rings O and O’ are put on two vertical stationery rods AB and A’B’ respectively. One end of an inextensible thread is tied at point A’. The thread passes through ring O’ and its other end is tied to ring O. Assuming that ring O’ moves downwards at a constant velocity ${{v}_{1}}$, then velocity ${{v}_{2}}$ of the ring O, when $\angle AOO'=\alpha$ is –

& \text{A) }{{\text{v}}_{1}}\left[ \dfrac{2{{\sin }^{2}}\dfrac{\alpha }{2}}{\cos \alpha } \right] \\\ & \text{B) }{{\text{v}}_{1}}\left[ \dfrac{2{{\cos }^{2}}\dfrac{\alpha }{2}}{\sin \alpha } \right] \\\ & \text{C) }{{\text{v}}_{1}}\left[ \dfrac{3{{\cos }^{2}}\dfrac{\alpha }{2}}{\sin \alpha } \right] \\\ & \text{D) None of these} \\\ \end{aligned}$$

Answer 1

We need to understand the relation between the velocity of the moving ring to the effect that causes a velocity on the other ring at a particular angle. We can easily solve this problem using the trigonometric relations involved in the situation.

Complete Step-by-Step Solution:
We are given a particular arrangement in which two rings are connected together by an inextensible thread on two rods as given in the figure. It is given that the ring O’ is moving downwards. In order to let this downward movement possible, the ring O should be moving upwards as the thread has a fixed length always.

We are asked to find the velocity at which the ring O will move upward at a point when the ring O is at an angle $\alpha$with the rod AB.

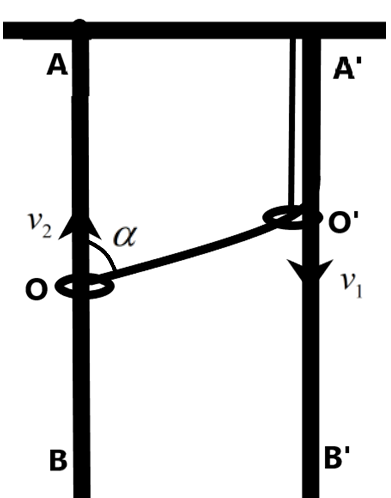
We know that the length of the wire from A’ to the O will be always constant. At an instant, if ‘x’ is the length of the wire from A’ to O’ and ‘y’ is the length from O’ to O, then –

& x+y=l \\\ & \text{differentiating with respect to time,} \\\ & \Rightarrow \dfrac{dx}{dt}+\dfrac{dy}{dt}=0 \\\ & \therefore {{v}_{1}}-{{v}_{2}}=0\text{ --(1)} \\\ \end{aligned}$$ The two velocities are in the opposite directions, so the sign is negative. Now, when was the second term in the above equation to be found. We can resolve the velocities given as shown in the below figure. 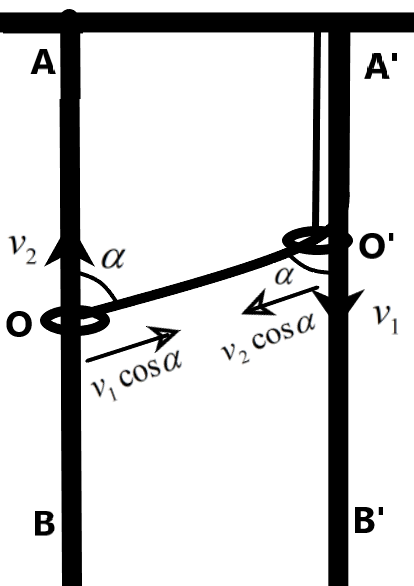 From the figure given above, we can understand that components of the two velocities along the horizontal direction add to the velocity of the ring O in the upward direction. We understand the cosine of the two velocities add up to the velocity of the ring O. It is given as – i.e., $$\begin{aligned} & {{v}_{2}}-{{v}_{1}}\cos \alpha ={{v}_{2}}\cos \alpha \\\ & \therefore {{v}_{2}}={{v}_{1}}\cos \alpha +{{v}_{2}}\cos \alpha \\\ \end{aligned}$$ But the two velocities are in the opposite directions from equation 1, so – $$\begin{aligned} & {{v}_{1}}\cos \alpha +{{v}_{2}}\cos \alpha ={{v}_{2}} \\\ & \text{but,} \\\ & {{\text{v}}_{1}}-{{v}_{2}}=0 \\\ & \Rightarrow {{v}_{1}}-({{v}_{1}}\cos \alpha +{{v}_{2}}\cos \alpha )=0 \\\ & \Rightarrow {{v}_{2}}={{v}_{1}}\dfrac{1-\cos \alpha }{\cos \alpha } \\\ & \therefore {{v}_{2}}={{\text{v}}_{1}}\left[ \dfrac{2{{\sin }^{2}}\dfrac{\alpha }{2}}{\cos \alpha } \right] \\\ \end{aligned}$$ This is the required velocity of ring O. **The correct answer is option A.** **Note:** In the given situation, we could take the distance OO’ as the varying parameter because the length of the thread from A’ passing through O’ to O is always a constant and the change in A’O’ is the velocity of the ring O’ moving downwards.