Question

Two small particles of mass m each are placed at the vertices A and B of a right angle isosceles triangle. If $AB = l$, find the gravitational field strength at C.

Answer 1

First, draw the diagram of the triangle with all the information. After this, use the Pythagoras to determine the distance of point C form points A and B. Then, we will use the expression of the gravitational field strength to determine its magnitude at C.

Complete step by step answer:
Draw the diagram of the triangle.

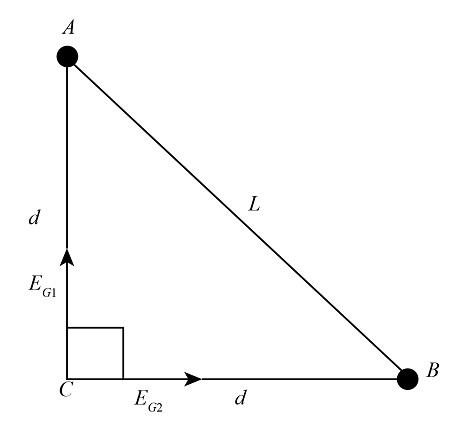
We know that C is equidistant from the points A and B. so we will use the Pythagoras theorem for the calculation of the distance of point C from point A and B.
Therefore, we get
{d^2} + {d^2} = {L^2}\\\
$\implies 2{d^2} = {L^2}\\\$
$\implies d = \dfrac{L}{{\sqrt 2 }}$ …… (1)
Here, $d$ is the distance of the point C from A and B, and $L$ is the distance between A and B.
Write the expression of the gravitational field strength at point C due to the particle present at point A, so
${E_{G1}} = \dfrac{{Gm}}{{{d^2}}}$
Here, $m$ is the mass of the particle at A, $G$ is the gravitational constant and $d$ is the distance of point C form the A.
From equation (1), substitute the value of $d$ in the above equation, so the above equation becomes
{E_{G1}} = \dfrac{{Gm}}{{{{\left( {\dfrac{L}{{\sqrt 2 }}} \right)}^2}}}\\\
$\implies {E_{G1}} = \dfrac{{2Gm}}{{{L^2}}}$ …… (2)
Similarly, write the expression of the magnetic field strength at C due to particle present at B, so
${E_{G2}} = \dfrac{{Gm}}{{{d^2}}}$
Here, $m$ is the mass of the particle at B, $G$ is the gravitational constant and $d$ is the distance of point C form the B.
From equation (1), substitute the value of $d$ in the above equation, so the above equation becomes
{E_{G2}} = \dfrac{{Gm}}{{{{\left( {\dfrac{L}{{\sqrt 2 }}} \right)}^2}}}\\\
$\implies {E_{G2}} = \dfrac{{2Gm}}{{{L^2}}}$ …… (3)
From the diagram, we know that the angle between ${E_{G1}}$ and ${E_{G2}}$ is 90 degrees, so the resultant of the ${E_{G1}}$ and ${E_{G2}}$ becomes,
$E = \sqrt {{{\left( {{E_{G1}}} \right)}^2} + {{\left( {{E_{G1}}} \right)}^2}}$
Substitute the values form equation (2) and (3) in the above equation.
Therefore, we get
E = \sqrt {{{\left( {\dfrac{{2Gm}}{{{L^2}}}} \right)}^2} + {{\left( {\dfrac{{2Gm}}{{{L^2}}}} \right)}^2}} \\\
$\implies E = \sqrt {2{{\left( {\dfrac{{2Gm}}{{{L^2}}}} \right)}^2}}$
$\implies E = \sqrt 2 \left( {\dfrac{{2Gm}}{{{L^2}}}} \right)$
$\implies \sqrt 2 \left( {\dfrac{{2Gm}}{{{L^2}}}} \right)$
Therefore, the gravitational field strength at C is $\sqrt 2 \left( {\dfrac{{2Gm}}{{{L^2}}}} \right)$.

Note:
Always draw the diagram of the given condition with the representation of distances between various points, direction of the gravitational field and other things for a better understanding of the solution. Also, remember the expression of the gravitational field strength.