Question

Two small particles of mass $m$ each are placed at the vertices A and B of a right-angled isosceles triangle. If $AB=b$, find the gravitational field strength at C.

Answer 1

First we need to determine the distances $AC$ and $BC$ . then we need to find out the gravitational field at C for them individually. As the gravitational field is a vector, then we need to apply the vector laws to find out the resultant gravitational field. We need to follow these steps to solve the problem.
Formula used:
$\begin{aligned} & 1)E=\dfrac{F}{m}=\dfrac{Gm}{{{r}^{2}}} \\\ & 2)R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta } \\\ \end{aligned}$

Complete step-by-step solution
Gravitational strength at any point is defined as gravitational force per unit mass. Mathematically, gravitational strength is represented by:
$E=\dfrac{F}{m}=\dfrac{Gm}{{{r}^{2}}}$
where
$E$ is the gravitational strength at a point
$F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}$ is the gravitational force acting on the point due to point masses ${{m}_{1}}$ and ${{m}_{2}}$ kept apart at a distance of $r$
$G$ is the gravitational constant
Let this be equation 1.

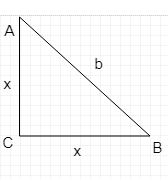
Now, let $AC=BC=x$
Applying Pythagoras’ theorem, we have
$\sqrt{{{x}^{2}}+{{x}^{2}}}=b\Rightarrow x=\dfrac{b}{\sqrt{2}}$
So, the gravitational strengths at C for the equal masses $m$ placed at A and B are individually given by:
$E=\dfrac{Gm}{{{(\dfrac{b}{\sqrt{2}})}^{2}}}=\dfrac{2Gm}{{{b}^{2}}}$
Let this be equation 2.
Now, these two forces act perpendicular to each other at C, as can be understood from the diagram below.

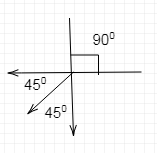
Therefore, using laws of vectors, the resultant gravitational strength at C is given by:
${{E}_{R}}=\sqrt{{{\left( \dfrac{2Gm}{{{b}^{2}}} \right)}^{2}}+{{\left( \dfrac{2Gm}{{{b}^{2}}} \right)}^{2}}+2{{\left(\dfrac{2Gm}{{{b}^{2}}}\right)}^{2}}\cos 90}=\dfrac{2\sqrt{2}Gm}{{{b}^{2}}}$
And this resultant gravitational strength will make ${{45}^{0}}$ angle with AC and BC.

Additional information: Here, we have calculated gravitational strength, which is vector quantity. If we had to calculate gravitational potential, then we would have used the formula gravitational potential as follows:
$\phi =\dfrac{Gm}{r}$
where $r$ is the distance of the point from the mass. It is a scalar quantity and thus we do not have to use the vector law.

Note: Whenever we are dealing with gravitational force or gravitational strength, we have to keep in mind that it is a vector quantity so we need to apply the laws of vectors to get the resultant field strength. Also, the gravitational force is independent of the medium. While calculating the field we must always be aware of which terms are under the roots, otherwise, our calculation will be wrong.