Question

Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are $\text{v}$ and $\text{2v}$ respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at A, these two particles will again reach the point A?

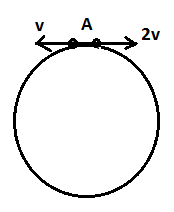
A. $4$
B. $3$
C. $2$
D. $1$

Answer 1

Here velocities of two particles and their path of travelling are given. It is asked to find the number of collisions before reaching the initial position. Since the particles travel in a circular path, we can find the distance travelled by the particles before each collision, using the formula for velocity. From the question we know that particles have elastic collisions. Then, they will interchange their velocities and directions at time of collision. Therefore, we can find the number of collisions by analyzing their travelling distance and directions.
Formula used:
$\text{Distance = velocity }\\!\\!\times\\!\\!\text{ time}$
$\text{Circumference of a circle = 2}\pi \text{R}$

Complete answer:
Let’s assume that the radius of the circular orbit is $R$ and the first collision takes place at time $t$
It is given that the two particles move with velocity $\text{v}$and$\text{2v}$.
Let’s say,
$\text{Velocity of particle 1, }{{\text{v}}_{1}}\text{= v}$
We have,
$\text{Distance = velocity }\\!\\!\times\\!\\!\text{ time}$
$\text{Distance travelled by particle 1, }{{\text{D}}_{\text{1}}}\text{ =vt}$
$\text{Velocity of particle 2, }{{\text{v}}_{2}}\text{= 2v}$
$\text{Distance travelled by particle 2, }{{\text{D}}_{2}}\text{ = 2vt}$
Total distance travelled by both the particles is the total circumference of the circle.
We have,
$\text{Circumference of a circle = 2}\pi \text{R}$
Then,
$\text{Total distance = 2}\pi \text{R}$
Therefore,
$\text{Total distance travelled by both the particles = }{{\text{D}}_{1}}\text{+}{{\text{D}}_{2}}\text{= vt}+2\text{vt}=2\pi R$
Then,
$t=\dfrac{2\pi R}{3v}$
Distance travelled by particle 1 is,
$\text{vt =v}\times \dfrac{\text{2 }\\!\\!\pi\\!\\!\text{ R}}{\text{3v}}=\dfrac{\text{2 }\\!\\!\pi\\!\\!\text{ R}}{3}$
And distance travelled by particle 2 is,
$\text{2vt =2v}\times \dfrac{\text{2 }\\!\\!\pi\\!\\!\text{ R}}{\text{3v}}=\dfrac{\text{4 }\\!\\!\pi\\!\\!\text{ R}}{3}$
From point A, particle 1 travels distance $\dfrac{\text{2 }\\!\\!\pi\\!\\!\text{ R}}{\text{3}}$and particle 2 travels distance$\dfrac{\text{4 }\\!\\!\pi\\!\\!\text{ R}}{\text{3}}$in time$t$. Hence, first collision occurs at point B.
After the 1st elastic collision these particles interchange their velocities and direction and continue travelling. The second elastic collision happens when they cover distances$\dfrac{\text{2 }\\!\\!\pi\\!\\!\text{ R}}{\text{3}}$and $\dfrac{\text{4 }\\!\\!\pi\\!\\!\text{ R}}{\text{3}}$ in time$\text{t}$. This happens at point C.

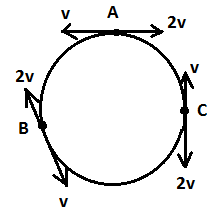
From figure, the first collision took place at point B, and the second collision at point C. After the second collision both the particles have their initial velocity and initial direction. And they cover another $\dfrac{\text{2 }\\!\\!\pi\\!\\!\text{ R}}{\text{3}}$and $\dfrac{\text{4 }\\!\\!\pi\\!\\!\text{ R}}{\text{3}}$distance in $\text{t}$time and third collision happens at point A. Hence before reaching the initial position A, the particles c

So, the correct answer is “Option C”.

Note:
Collision occurs when two objects come in contact with each other for a very short period. Here the momentum and energy of the colliding particles changes. If total momentum, the total energy and the total kinetic energy of colliding particles are conserved, then it is known as an elastic collision. When the mass of both the particles are equal, then during the elastic collision, the particles will exchange their velocities. When the mass of both the particles is the same, exchange of momentum between two particles is the maximum during the collision.