Question

Two small conducting balls having radius $R$ and $2R$ are given charges $-q$ and $2q$ respectively. When balls are placed at separation $r (r >> R)$ they attract each other with force $F$. If balls are connected by a conducting wire now they repel each other by force $\frac{F}{n}$, find $n$.

Answer 1

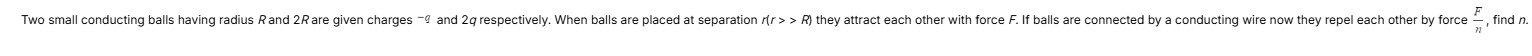
9

Answer 2

The initial charges on the two small conducting balls of radii $R$ and $2R$ are $-q$ and $2q$ respectively. The separation between the balls is $r$, where $r >> R$. Since the separation is much larger than the radii, we can treat the balls as point charges located at their centers.

The initial force between the balls is attractive because the charges have opposite signs. The magnitude of this force is given by Coulomb's Law:

$F = k \frac{|(-q)(2q)|}{r^2} = k \frac{|-2q^2|}{r^2} = k \frac{2q^2}{r^2}$

where $k = \frac{1}{4\pi\epsilon_0}$ is Coulomb's constant.

When the two conducting balls are connected by a conducting wire, charge flows between them until they reach the same electric potential. The total charge is conserved. The total charge is $Q_{total} = -q + 2q = q$.

Let the final charges on the spheres of radius $R$ and $2R$ be $q_1'$ and $q_2'$.

The total charge is distributed between the two spheres: $q_1' + q_2' = q$.

For conducting spheres far apart ($r >> R$), the potential of a sphere of radius $R'$ carrying charge $Q'$ is approximately $V = k \frac{Q'}{R'}$.

When connected, the potentials are equal: $V_1' = V_2'$.

$k \frac{q_1'}{R} = k \frac{q_2'}{2R}$

$\frac{q_1'}{R} = \frac{q_2'}{2R}$

$q_1' = \frac{q_2'}{2}$

Now we solve the system of equations for $q_1'$ and $q_2'$:

1. $q_1' + q_2' = q$

2. $q_1' = \frac{q_2'}{2}$

Substitute (2) into (1):

$\frac{q_2'}{2} + q_2' = q$

$\frac{3q_2'}{2} = q$

$q_2' = \frac{2q}{3}$

Now find $q_1'$ using (2):

$q_1' = \frac{1}{2} q_2' = \frac{1}{2} \left(\frac{2q}{3}\right) = \frac{q}{3}$

So, after connecting and removing the wire, the sphere with radius $R$ has charge $\frac{q}{3}$ and the sphere with radius $2R$ has charge $\frac{2q}{3}$. Both charges are positive, so the force between the spheres will be repulsive.

The magnitude of the final repulsive force $F'$ is given by Coulomb's Law:

$F' = k \frac{|q_1' q_2'|}{r^2} = k \frac{\left(\frac{q}{3}\right)\left(\frac{2q}{3}\right)}{r^2} = k \frac{\frac{2q^2}{9}}{r^2} = k \frac{2q^2}{9r^2}$

We are given that the final repulsive force is $\frac{F}{n}$.

$F' = \frac{F}{n}$

Substitute the expressions for $F'$ and $F$:

$k \frac{2q^2}{9r^2} = \frac{1}{n} \left(k \frac{2q^2}{r^2}\right)$

Assuming $q \neq 0$, we can cancel the common terms $k$ and $\frac{2q^2}{r^2}$ from both sides:

$\frac{1}{9} = \frac{1}{n}$

$n = 9$