Question

Two small blocks of equal mass are attached as shown in the figure. They are set into rotation on a horizontal frictionless plane at constant angular speed. The ratio $\dfrac{{{T_1}}}{{{T_2}}}$ is:

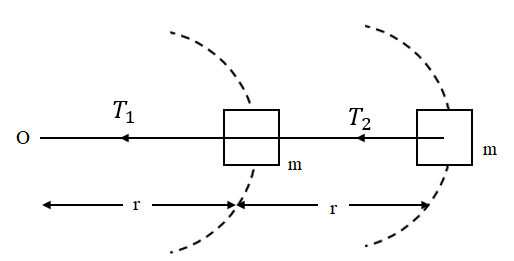
A. 2
B. 2/3
C. 1/2
D. 3/2

Answer 1

Find the tension in the string for both masses separately. This tension force is responsible for the circular motion of these masses. Therefore, we balance the centripetal force with the tension in the mass for respective masses.

Formula Used:
The centripetal force on the mass m in terms of angular velocity $\omega$ is given as,
${F_C} = mr{\omega ^2}$

Complete step by step answer:
We have to consider the separate rotation of both masses. We can see the first mass is revolving at a distance r from the centre O and the second mass is revolving at a distance 2r from the centre O. We can observe the necessary centripetal force for the rotation of first mass is provided by the tension in the string, which is ${T_1} - {T_2}$ and the necessary centripetal force for the rotation of the second mass is provided by the tension ${T_2}$.

We know that the centripetal force on the mass m in terms of angular velocity $\omega$ is given as,
${F_C} = mr{\omega ^2}$
Therefore, for the first mass, we can write,
${T_1} - {T_2} = mr{a^2}$ …… (1)
Here, a is the angular speed of the mass m as given in the question.

For the second mass, we can write,
${T_2} = m\left( {2r} \right){a^2}$ …… (2)
Divide equation (1) by equation (2).
$\dfrac{{{T_1} - {T_2}}}{{{T_2}}} = \dfrac{{mr{a^2}}}{{m\left( {2r} \right){a^2}}}$
$\Rightarrow \dfrac{{{T_1}}}{{{T_2}}} - 1 = \dfrac{1}{2}$
$\Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{1}{2} + 1$
$\Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{3}{2}$

Therefore, the correct answer is option (D).

Note: We have chosen the negative x-direction as the positive for the measure of direction of tension in the string. Therefore, if any force acts on the mass in positive x-direction, you should assume it has negative direction.