Question

Two small balls, each having equal positive charge Q are suspended by two insulating strings of equal length L from a hook fixed to a stand. If the mass of each ball = m & total angle between two strings is 60$^\circ$, then find the charge on each ball.

Answer 1

Hint: In this question, we have two types of forces working. One is Coulomb force due to charge on masses and other one is tension in the strings due to mass of the balls. By equating expressions for these forces, we can find the value of charge on the balls.

Step by step answer:
We have two balls with charge q exerting Coulomb force on each other given by following expression:

${F_C} = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q^2}}}{{{d^2}}}$

Since, both the charges are opposite, the two balls repel each other.

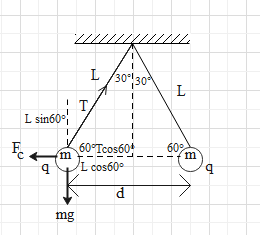
Due to the gravitational force on balls, they are pulled downwards by force mg which creates tension T in the string. This tensional force can be resolved into horizontal component:

$T\cos 60^\circ$ and vertical component: $T\sin 60^\circ$

$\therefore T\sin 60^\circ = mg \\\ \dfrac{{\sqrt 3 T}}{2} = mg{\text{ }}...{\text{(i)}} \\\$

Therefore, distance between two balls is $d = 2l\cos 60^\circ$

$\therefore {F_C} = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q^2}}}{{{{\left( {2l\cos 60^\circ } \right)}^2}}} \\\ \Rightarrow {F_C} = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q^2}}}{{4{l^2} \times \dfrac{1}{4}}} = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q^2}}}{{{l^2}}}{\text{ }}...{\text{(ii)}} \\\$

In equilibrium, that is, when Coulomb force balances the tensional force, the balls are at rest. At this point, the Coulomb force between the charges is equal and opposite to the horizontal component of tension. This means that they have equal magnitude and we can write the following relation for this condition.

${F_C} = T\cos 60^\circ = \dfrac{T}{2}{\text{ }}...{\text{(iii)}}$

Substituting the expression (ii) in (iii), we get
$\dfrac{T}{2} = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q^2}}}{{{l^2}}}{\text{ }}...{\text{(iv)}}$

Dividing (i) by (iv), we get

$\dfrac{{\sqrt 3 T}}{2} \times \dfrac{2}{T} = \dfrac{{4\pi { \in _0}mg{l^2}}}{{{q^2}}} \\\ \Rightarrow \sqrt 3 = \dfrac{{4\pi { \in _0}mg{l^2}}}{{{q^2}}} \\\ \Rightarrow {q^2} = \dfrac{{4\pi { \in _0}mg{l^2}}}{{\sqrt 3 }} \\\ \Rightarrow q = \sqrt {\dfrac{{4\pi { \in _0}mg{l^2}}}{{\sqrt 3 }}} \\\$

This is the required value of charge on each ball.

Note: We equate the various forces in terms of their magnitude not their direction. In this question, the forces that we have equated were in the opposite direction. So, if we write them in vector notation, then we will have to include the information of their direction also.