Question

Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rod of length L. They are placed on a frictionless horizontal surface. Another ball of mass 2 m moving with speed u towards one ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown in the figure.

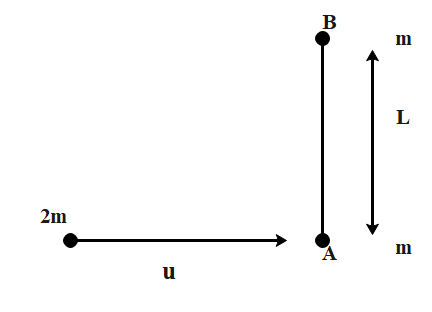
If the coefficient of restitution is ½, then the angular speed of the rod after collision will be
(A) $\dfrac{4}{3}\dfrac{u}{l}$
(B)$\dfrac{u}{l}$
(C) $\dfrac{2}{3}\dfrac{u}{l}$
(D) None of these

Answer 1

Whenever two particles hit each other, there’s a phenomenon called collision which is taking place between the particles. Similarly, when two balls hit each other, collision happens between the two balls. Wherever collision is occurring, the law of conservation of momentum is applicable.

Complete step-by-step answer:
By the law of conservation of momentum,
Initial momentum before collision = final momentum after collision
By Newton’s law of collision,
$e=\dfrac{\text{relative velocity of seperation}}{\text{relative velocity of approach}}$
Where, e is the coefficient of restitution
Angular speed of rod,
$\omega =\dfrac{\text{tangnetial velocity}}{\text{perpendicular distance}}$
The given data are
Mass of ball A which is equal to m. Mass of ball B which is equal to m. The length of rod the rod which is equal to L.
Another ball of mass m moving towards ball A with velocity u. That is, another ball collides with ball A.

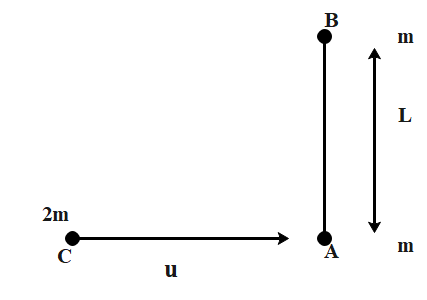
Let the other ball moving towards one of the two balls be C.
Therefore, the ball C is moving towards the ball A.
Here,
Initial velocity of ball A is zero. And, initial velocity of ball B is zero. Initial velocity of ball C is u.
Let the final velocities be like
Final velocity of ball C be ${{v}_{2}}$
And,
Final velocity of ball A be ${{v}_{1}}$.
When the collision ends, the final velocity of ball B will be zero. We know that as per the law of conservation of momentum, initial momentum before collision is equal to the final momentum after collision. Initial momentum before collision is equal to 2 mu
Final momentum after collision is the sum of momentums with respect to ${{v}_{1}}$ and ${{v}_{2}}$.
Let us apply the values of Initial momentum before collision and the Final momentum after collision in the law of conservation of momentum
We obtain an equation as,
$2mu=m{{v}_{1}}+2m{{v}_{2}}$---- (1)
Let this be equation (1)
Dividing equation (1) by 2m
We get,
$u=\dfrac{{{v}_{1}}}{2}+{{v}_{2}}$ ---- (2)
Let this be equation (2)
As per the Newton’s law of collision,
we know that coefficient of restitution,
$e=\dfrac{\text{relative velocity of seperation}}{\text{relative velocity of approach}}$
$\dfrac{1}{2}=\dfrac{{{v}_{1}}\text{ }{{v}_{2}}}{u}$----- (3)
Let this be equation (3)
Multiplying the above equation by 2u, we get,
$u=2({{v}_{1}}\text{ }{{v}_{2}})$ ----- (4)
Let this be equation (4)
Now, let us solve the equations (2) and (4),
We get,
${{v}_{1}}+\text{ }{{v}_{2}}=2({{v}_{1}}\text{ }{{v}_{2}})$
${{v}_{1}}+\text{ }{{v}_{2}}=2{{v}_{1}}\text{ 2}{{v}_{2}}$
$\text{2}{{v}_{2}}+\text{ }{{v}_{2}}=2{{v}_{1}}{{v}_{1}}\text{ }$
$\text{3 }{{v}_{2}}={{v}_{1}}\text{ }$ ----- (5)
Let this be equation (5)
Substitute equation (5) in equation (4),we get,
$\text{u=2(3 }{{v}_{2}}-{{v}_{2}})\text{ }$
$\text{u=2(2}{{v}_{2}})\text{ }$
$\text{u=4}{{v}_{2}}\text{ }$ ---- (6)
Let this be equation (6)
Velocity of ball B is zero just after collision
That is, ${{v}_{2}}=0$---- (7)
Let this be equation (7)
Now, substitute equation (7) in (6)
We get,
u=0--- (8)
Let this be equation (8)
We know that the angular speed of rod
$\omega =\dfrac{\text{tangential velocity}}{\text{perpendicular distance}}$
In this problem, tangential velocity is u and, the perpendicular distance is l.
Since u =0
Angular speed of the rod after collision will be zero
That is, we get
$\omega =0$
Of the choices given in the question, the value we obtained is not given.
Therefore, the answer is
(D) None of these.

So, the correct answer is “Option D”.

Note: The value of the angular speed of the rod after collision differs for different situations.
For example, If u is not equal to zero, angular speed of the rod after collision is,
$\omega =\dfrac{u}{l}$