Question

Two similar conducting balls having charges $+q$ and $-q$ are placed at a separation d from each other in air. The radius of each ball is r and the separation between their centres is d (d >> r). Calculate the capacitance of the two-ball system.

A. $4\pi \epsilon_0 r$
B. $2\pi \epsilon_0 r$
C. $4\pi log_e\dfrac{\epsilon_0 r}{d}$
D. $4\pi log_e\dfrac{ r}{d}$

Answer 1

Recall that the storage of charge is possible only when there is a potential difference across the conductors. Thus, calculate the difference in potential between the two balls of the system. Following this we know that the capacitance is the ratio of the magnitude of charge in the system and the potential difference across the conductors in the system. Use this to ultimately determine the capacitance of the two-ball system and arrive at the appropriate result.

Formula used: Capacitance $C = \dfrac{Q}{V_A – V_B}$
Potential $V = \dfrac{1}{4\pi\epsilon_0}\dfrac{Q}{r}$

Complete step by step answer:
We know that capacitance C or the electrical capacity of a system of conductors is the ability of the system to store electric charge. It is given as the ratio of the charge Q stored in the system to the potential difference V between the components of the system:
$C = \dfrac{Q}{V}$
In the context of our question, we are given that we have two balls A and B with charges $+q$ and $-q$ respectively. We know that a potential difference across conductors arises whenever there is a difference in the electronegativity across the conductors. The difference in the charges across the two balls gives rise to a potential difference between them.

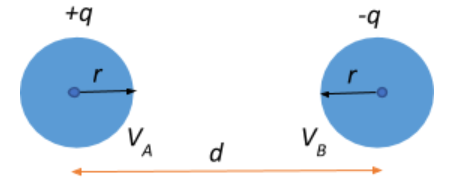
If the potential at A due to charges $+q$ is $V_A$ and the potential at B due to charges $-q$ is $V_B$, then the potential difference across the two balls is given as:
$V = V_A-V_B$
We know that for a sphere carrying a charge, all its charge is distributed evenly about the surface of the sphere. Thus, the potential of the sphere arises from the distribution of charges about the spherical surface, all at a distance r from the centre of the sphere. This is given as:
$V = \dfrac{1}{4\pi\epsilon_0}\dfrac{Q}{r}$, where $\epsilon_0$ is the permittivity of free space, Q is the charge on the sphere, and r is the radius of the sphere.
Thus, in the case of the two charged balls given to us, the charges that they carry are distributed about the surface of the ball all at a radial distance r from the centre. Therefore, the potential of the balls can be given as:
$V_A = \dfrac{1}{4\pi\epsilon_0}\dfrac{(+q)}{r}$ and $V_B=\dfrac{1}{4\pi\epsilon_0}\dfrac{(-q)}{r}$
The potential difference across the two balls that contributes to the potential energy of the system and consequently the charge storage capacity or capacitance of the system is thus obtained to be:
$V = V_A-V_B = = \dfrac{1}{4\pi\epsilon_0}\dfrac{(+q)}{r} - \dfrac{1}{4\pi\epsilon_0}\dfrac{(-q)}{r} = \dfrac{1}{4\pi\epsilon_0 r}.(q-(-q)) = \dfrac{2q}{4\pi\epsilon_0 r} = \dfrac{q}{2\pi\epsilon_0 r}$
Consequently, the capacitance of this system of conductors arising due to this potential difference is given as:
$C = \dfrac{Q}{V} = \dfrac{q}{\dfrac{q}{2\pi\epsilon_0 r}} = 2\pi\epsilon_0 r$

So, the correct answer is “Option B”.

Note: From the above analysis we see that the capacitance of the two-ball system would surprisingly remain the same irrespective of the distance between them. This is because the distance between them is responsible only for creating a potential difference between them (since if they were to come in contact or be connected by a wire there would be a flow of charges until both spheres had the same charge leading to no potential difference), whereas the charge carrying capacity of the balls arises only due to the size of the spheres and the distribution of charges about their structure. This is why we considered the radius r of the spheres to which the charges are confined and not the distance between the spheres where no charges exist, while calculating the potential.