Question

Two similar coils of radius $R$ are lying concentrically with their planes at right angles to each other. The currents flowing in them are $I$ and $2I$ respectively. The resultant magnetic field induction at the center will be:
(A) $\dfrac{{{\mu _0}I}}{{2R}}$
(B) $\dfrac{{{\mu _0}I}}{R}$
(C) $\dfrac{{\sqrt 5 {\mu _0}I}}{{2R}}$
(D) $\dfrac{{3{\mu _0}I}}{{2R}}$

Answer 1

Hint : Here, the magnetic field is the area around a magnet in which there is magnetic force. The moving electric charges can make magnetic fields. Two coils of radius $R$ are concentric with their planes at right angles to each other and we have to calculate the resultant magnetic field induction at the center by using formula of magnetic field at the center of the coil given by:
$B = \dfrac{{{\mu _0}nI}}{{2a}}$ ; The $n$ is the no. of turns of the coil, $I$ is the current and $a$ is the radius of the coil.
Using this formula we have to find the resultant magnetic field induction.

Complete Step By Step Answer:
Here, we have been given the two coils perpendicular to each other as shown in figure below:

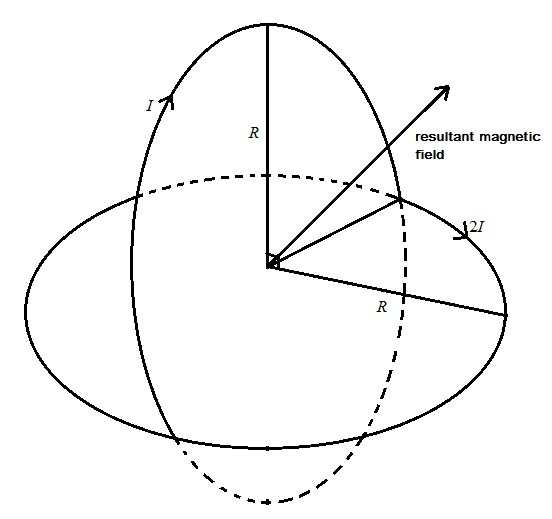
From the figure we have to draw the magnetic field at the center of the coil with magnetic field ${B_1}$
${B_1}$ is to be calculated by the magnetic field induction formula $B = \dfrac{{{\mu _0}nI}}{{2a}}$
Therefore,
${B_1} = \dfrac{{{\mu _0}I}}{{2R}}$ ......…. (Number of turns is $n = 1$ ) $(1)$
Magnetic field at center due to second coil perpendicular to the first coil is given by ${B_2}$
${B_2} = \dfrac{{{\mu _0}\left( {2I} \right)}}{{2R}}$ …. $(2)$
Hence, from $(1)$ and $(2)$ , we get
The net magnetic field at the center $= \sqrt {{B_1}^2 + {B_2}^2}$
$= \dfrac{{\sqrt 5 {\mu _0}I}}{{2R}}$
Thus, the resultant magnetic field induction is calculated as $\dfrac{{\sqrt 5 {\mu _0}I}}{{2R}}$
The correct answer is option C.

Note :
The resultant magnetic field induction at center is obtained by the formula we have used above. This formula is for $n$ no. of turns of the coil but here we know here that the coil is of one turn only. The net magnetic field is calculated as the square root of the sum of the squares of magnetic fields of two coils.