Question

Two similar coils of radius R and numbers of turns N are lying concentrically with their planes at right angles to each other. The currents flowing in them are $I$ and $I\sqrt 3$ respectively. Then the resultant magnetic induction at the center will be:
A. $\dfrac{{{\mu _0}NI}}{{2R}}$
B. $\dfrac{{{\mu _0}NI}}{R}$
C. $\sqrt 3 \dfrac{{{\mu _0}NI}}{{2R}}$
D. $\sqrt 5 \dfrac{{{\mu _0}NI}}{{2R}}$

Answer 1

Hint: We know that when two magnetic fields are perpendicular to each other then their resultant magnetic induction is found with the help of Biot-Savart’s Law so use this concept to reach the solution of the question.

Complete step-by-step solution -

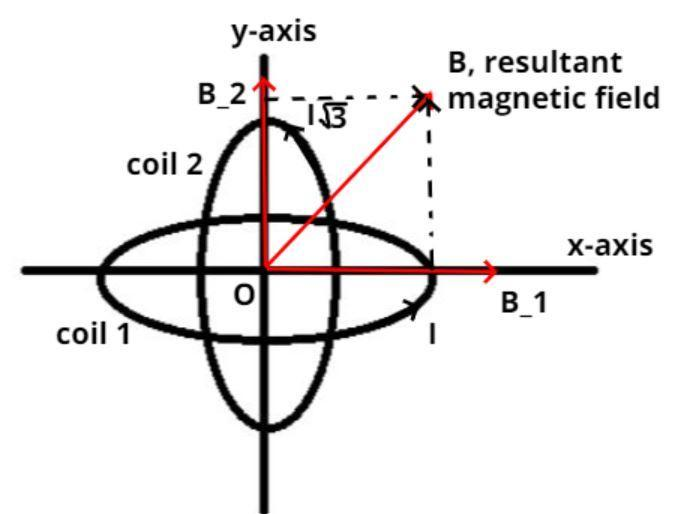
It is given that the two coils are the same having radius R and number of turns N and carrying current $I$ but lying concentrically (i.e. same center) with their planes at right angle w.r.t each other as shown in the figure.
Here, in the first coil which is directed towards x-axis current $I$ is flowing as shown in the figure.
So, magnetic field due to this coil carrying current I at the center ${B_1} = \dfrac{{{\mu _0}NI}}{{2R}}$
Now, magnetic field due to other coil which is directed towards y-axis carrying current $I\sqrt 3$ at the center as shown in the figure, ${B_2}$= $\dfrac{{{\mu _0}NI\sqrt 3 }}{{2R}}$
Now, resultant magnetic field according to phasor sum it is calculated as
$\Rightarrow B = {B_1}\hat i + {B_2}\hat j$
Where, $\hat i$ and $\hat j$ are the unit vectors along x and y-axis respectively.
Now take the magnitude of the resultant field we have,
$\Rightarrow B = \sqrt {{B_1}^2 + {B_2}^2}$
Now substitute the values we have,
$\Rightarrow B = \sqrt {{{\left( {\dfrac{{{\mu _0}IN}}{{2R}}} \right)}^2} + {{\left( {\dfrac{{{\mu _0}I\sqrt 3 }}{{2R}}} \right)}^2}}$
Now simplify this we have,
$\Rightarrow B = \dfrac{{{\mu _0}IN}}{R}\sqrt {\dfrac{1}{4} + \dfrac{3}{4}} = \dfrac{{{\mu _0}IN}}{R}\sqrt {\dfrac{4}{4}} = \dfrac{{{\mu _0}IN}}{R}$
$\Rightarrow B = \dfrac{{{\mu _0}NI}}{R}$
So this is the required answer.

Hence option (B) is the correct answer.

Note: Biot- Savart Law is used to determine the strength of magnetic field at any point due to a current carrying conductor. So due to the first coil there is a magnetic field $B_1$ and due to the second coil $B_2$. In this question we have to find out net magnetic induction at the center of the coil. Thus we are taking out the resultant magnetic field for the system of two concentric current carrying coils.