Question

Two similar coils are kept mutually perpendicular such that their centers coincide. At the center, find the ratio of the magnetic field due to one coil and the resultant magnetic field through both coils, if the same current is flown.

Answer 1

The magnetic field defines the magnetic effect in the relative motion of electric charges and magnetic materials. A charge which travels parallel to other charges current will experience a force perpendicular to its velocity.

Complete step by step solution:

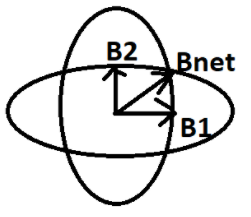
We can take the magnetic field produced in one coil as ${B_1}$ and the magnetic field produced by the other coil as${B_2}$. The net magnetic field produced by the two coils is ${B_{net}}$. It is said that two coils are similar to each other and they are kept mutually perpendicular.
Therefore we can write it as,${B_1} = {B_2} = B$
Since the two coils are perpendicular to each other the angle between them will be ${90^0}$.
Therefore the resultant magnetic field is given as
$= \sqrt {{B^2} + {B^2} + 2B.B\cos {{90}^ \circ }}$
$= \sqrt {2{B^2}}$ (Since cos${90^ \circ }$=0)
$= B\sqrt 2$
Therefore the ratio between the magnetic field due to one coil and the resultant magnetic field through both coils will be,
$\dfrac{B}{{B\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}$
Therefore the ratio will be $1:\sqrt 2$
The correct option is A.

Note:
The magnetic field can be expressed in two different ways. One is magnetic field vectors and the other is magnetic field lines. When we describe the magnetic field mathematically it is called magnetic field vectors. This vector field can be directly plotted as many sets of vectors are drawn on a grid. Each vector will point in the direction that a compass points. And it has a length that is dependent on the strength of the magnetic force. The other method to represent the magnetic field is magnetic field lines. Here we eliminate the grid pattern and connect all the vectors with smooth lines.