Question

Two similar balls of mass ‘ ${\text{m}}$ ’ are hung by a silk thread of length ${\text{L}}$ and carry similar charges ${\text{Q}}$ as in figure. Assuming the separation to be small, the separation between the balls (denoted by x) is equal to ________

Answer 1

To solve this problem, we need to find the distance between both the masses. We should simply balance the forces on masses with charge ${\text{Q}}$ .

Formula used:
We would be using the Coulomb’s law:
${\text{F }}\dfrac{{{\text{K}}{{\text{q}}_{\text{1}}}{{\text{q}}_{\text{2}}}}}{{{{\text{r}}^{\text{2}}}}}$
Here, ${\text{F}}$ is the force between the masses
${\text{k}}$ is the Coulomb’s constant
${{\text{q}}_{\text{1}}}{\text{,}}{{\text{q}}_{\text{2}}}$ are the charges
${\text{r}}$ is the distance between the charges.

Complete step by step answer:
Let us assume that, initially the masses are hung with their respective charges and tension ${\text{T}}$ is acting on the silk thread holding them.

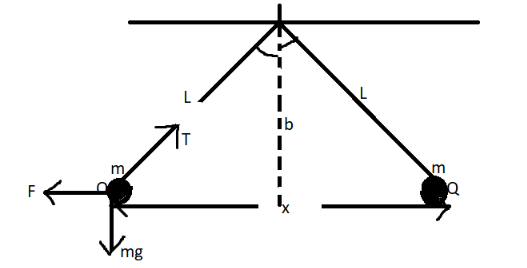
On resolving the forces in vertical and horizontal direction:
${\text{Tsin}}\theta {\text{ = F}}$
${\text{Tcos}}\theta {\text{ = mg}}$ .
By Pythagoras theorem, in the triangle above:
${\left( {\dfrac{{\text{x}}}{{\text{2}}}} \right)^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}{\text{ = }}{{\text{L}}^{\text{2}}}$
$\Rightarrow {\text{b = }}{\sqrt {\text{L}} ^{\text{2}}}{\text{ = L}}$
On applying Coulomb’s law,
${\text{F = }}\dfrac{{{\text{K}} \times {\text{Q}} \times {\text{Q}}}}{{{{\text{x}}^{\text{2}}}}}$
Now, putting these values in the resolved equations,
$\Rightarrow \dfrac{{{\text{Tsin}}\theta }}{{{\text{Tcos}}\theta }}{\text{ = }}\dfrac{{\text{F}}}{{{\text{mg}}}}$
$\Rightarrow {\text{mg}}\left( {\dfrac{{{\text{sin}}\theta }}{{{\text{cos}}\theta }}} \right){\text{ = }}\dfrac{{{\text{K}}{{\text{Q}}^{\text{2}}}}}{{{x^{\text{2}}}}}$
On putting the values of sine and cosine from the triangles as given in the figure:
$\Rightarrow {\text{mg}}\left( {\dfrac{{\text{x}}}{{{\text{2L}}}}} \right){\text{ = }}\dfrac{{{\text{K}}{{\text{Q}}^{\text{2}}}}}{{{{\text{r}}^{\text{2}}}}}$
$\Rightarrow {\text{mg}}\left( {\dfrac{{{{\text{x}}^{\text{3}}}}}{{{\text{mg}}}}} \right){\text{ = }}\dfrac{{{\text{K}}{{\text{Q}}^{\text{2}}} \times {\text{2L}}}}{{\text{1}}}$
On putting the value of, ${\text{K = }}\dfrac{{\text{1}}}{{{\text{4}}\pi {\varepsilon _{\text{0}}}}}$
${\text{x = }}{\left( {\dfrac{{\text{1}}}{{{\text{4}}\pi {\varepsilon _{\text{0}}}}}\dfrac{{{{\text{Q}}^{\text{2}}}{\text{L}}}}{{{\text{mg}}}}} \right)^{{\text{1/3}}}}$
So, the distance between the masses is ${\text{x = }}{\left( {\dfrac{{\text{1}}}{{{\text{4}}\pi {\varepsilon _{\text{0}}}}}\dfrac{{{{\text{Q}}^{\text{2}}}{\text{L}}}}{{{\text{mg}}}}} \right)^{{\text{1/3}}}}$ .

Additional Information
Coulomb's law, or Coulomb's inverse-square law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is conventionally called electrostatic force or Coulomb force. The law was first discovered in 1785 by French physicist Charles-Augustin de Coulomb, hence the name. Coulomb's law was essential to the development of the theory of electromagnetism

Note:
We should also note that the value of K should always be replaced to cancel other values. Also, the force is along the straight line joining the two charges. If the charges have the same sign, the electrostatic force between them is repulsive; if they have different signs, the force between them is attractive.