Question

Two sides of a triangle are in the ratio 3 : 5 and the third side is 16. If $\Delta$ is the largest possible area of the triangle, then $\frac{\Delta}{20}=$

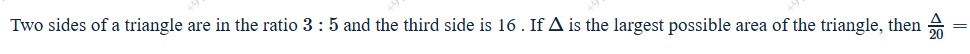
Answer 1

6

Answer 2

We are given a triangle with sides in the ratio $3:5$ (let these be $3x$ and $5x$) and the third side is $16$. We wish to maximize the area $\Delta$ (and then compute $\Delta/20$).

Step 1. Write the Semiperimeter and Heron Formula

For sides $3x$, $5x$, and $16$:

$$s = \frac{3x + 5x + 16}{2} = 4x + 8.$$

By Heron’s formula, the area is:

$$\Delta = \sqrt{s(s-3x)(s-5x)(s-16)}.$$

Substitute:

$$\Delta = \sqrt{(4x+8)(4x+8-3x)(4x+8-5x)(4x+8-16)}.$$

This simplifies to:

$$\Delta = \sqrt{(4x+8)(x+8)(8-x)(4x-8)}.$$

Step 2. Simplify the Expression

Factor where possible:

$$4x+8 = 4(x+2)\quad\text{and}\quad 4x-8 = 4(x-2).$$

Then:

$$\Delta = \sqrt{4(x+2) \cdot (x+8) \cdot (8-x) \cdot 4(x-2)} = \sqrt{16\,(x+2)(x-2)(x+8)(8-x)}.$$

Note that:

$$(x+2)(x-2) = x^2-4,\quad (x+8)(8-x) = 64 - x^2.$$

Thus:

$$\Delta^2 = 16\,(x^2-4)(64-x^2).$$

Step 3. Maximize the Area

Let:

$$f(x) = (x^2-4)(64-x^2).$$

Introduce $u = x^2$ so that:

$$f(u) = (u-4)(64-u) = -u^2 + 68u - 256.$$

The quadratic $-u^2 +68u -256$ is concave downward. Its maximum occurs at:

$$u = \frac{68}{2} = 34 \quad \Longrightarrow \quad x^2 = 34 \quad \Longrightarrow \quad x = \sqrt{34} \;(\text{since } x>0).$$

Thus, maximum value:

$$f_{\max} = (34-4)(64-34) = 30 \times 30 = 900.$$

Then:

$$\Delta_{\max}^2 = 16 \times 900 = 14400 \quad \Longrightarrow \quad \Delta_{\max} = \sqrt{14400} = 120.$$

Step 4. Final Answer

We are asked for:

$$\frac{\Delta_{\max}}{20} = \frac{120}{20} = 6.$$