Question

Two sides of a triangle are 4m and 5m in length and the angle between them is increasing at a rate of 0.06rad/sec. Find the rate at which the area of the triangle is increasing when the angle between the sides of the fixed-length is $\dfrac{\pi }{3}$.

Answer 1

Here we have been given the length of two fixed sides and the rate of change of angle between these lines and then we have been asked to find the rate of the change in the area of the triangle when the angle between these lines is $\dfrac{\pi }{3}$. For this, we will use the formula of the area of a triangle with two fixed sides of length ‘a’ and ‘b’ and $\alpha$ is the angle between them given as $area=\dfrac{1}{2}ab\sin \alpha$. Then we will differentiate this with respect to time on both sides after keeping the given values from the question in this formula. After differentiating, we will keep the value of the given angle between them and hence we will find the required rate of change in the area of the triangle.

Complete step-by-step solution:
We here have been given that two sides of the fixed length of the triangle are 4m and 5m. Let us assume the angle between these lines to be $\theta$. The triangle is shown below:

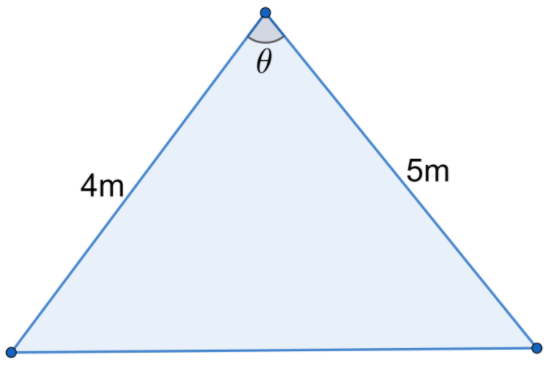
Now, we know that if ‘a’ and ‘b’ are the lengths of two sides of any triangle and the angle between those sides is $\alpha$, then the area of the triangle is given as:
$area=\dfrac{1}{2}ab\sin \alpha$
Here, we can see that:
a=5m
b=4m
$\alpha =\theta$
Thus, if we assume the area to be ‘A’, then the required area is given as:
$\begin{aligned} & A=\dfrac{1}{2}\left( 5 \right)\left( 4 \right)\sin \theta \\\ & \Rightarrow A=\dfrac{20}{2}\sin \theta \\\ & \Rightarrow A=10\sin \theta \\\ \end{aligned}$
Now, if we differentiate this area with respect to time, i.e. ‘t’, we will get the rate of change in area.
Thus, differentiating A w.r.t. t we get:
$\begin{aligned} & A=10\sin \theta \\\ & \Rightarrow \dfrac{dA}{dt}=10\cos \theta \dfrac{d\theta }{dt} \\\ \end{aligned}$
Now, here we have been given that $\dfrac{d\theta }{dt}=0.06radian/\sec$.
Thus, we get the rate of change of area as:
$\begin{aligned} & \dfrac{dA}{dt}=10\cos \theta \dfrac{d\theta }{dt} \\\ & \Rightarrow \dfrac{dA}{dt}=10\cos \theta \left( 0.06 \right) \\\ & \Rightarrow \dfrac{dA}{dt}=0.6\cos \theta \\\ \end{aligned}$
Now, here we have been asked to find the rate of change in area when $\theta =\dfrac{\pi }{3}$.
Thus, we get the required rate as:
$\begin{aligned} & \dfrac{dA}{dt}=0.6\cos \theta \\\ & \Rightarrow \dfrac{dA}{dt}=0.6\cos \dfrac{\pi }{3} \\\ & \Rightarrow \dfrac{dA}{dt}=0.6\left( \dfrac{1}{2} \right) \\\ & \therefore \dfrac{dA}{dt}=0.3{{m}^{2}}/\sec \\\ \end{aligned}$
Hence, the required rate of change in area is $0.3{{m}^{2}}/\sec$.

Note: We here have used the formula $area=\dfrac{1}{2}ab\sin \alpha$. This formula is derived as follows:
Let us assume a triangle ABC, with height AD.

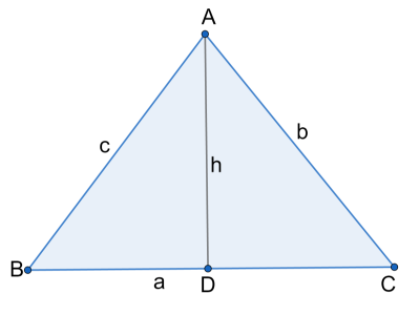
Now, we can see from the figure that AB=c, BC=a, CA=b, and AD=h.
Now, we know that the area of any triangle is given as:
$area=\dfrac{1}{2}\times base\times height$
Here,
Base=a
Height=h
Thus, we have:
$area=\dfrac{1}{2}ah$
Now, if we consider $\Delta ADC$, we can see that:
$\dfrac{h}{b}=\sin C$
Thus, we get the area as:
$\begin{aligned} & area=\dfrac{1}{2}ah \\\ & \Rightarrow area=\dfrac{1}{2}a\left( b\sin C \right) \\\ & \Rightarrow area=\dfrac{1}{2}ab\sin C \\\ \end{aligned}$