Question

Two sides of a parallelogram are along the lines $x+y=3$ and $x-y+3=0$. If its diagonals
intersect at $(2,4)$, then one of its vertex is
(a) $(2,6)$
(b) $(2,1)$
(c) $(3,5)$
(d) $(3,6)$

Answer 1

Hint: Solve the 2 line equations to find the coordinates of intersection of these 2 lines and use section formula to find the remaining coordinates of a parallelogram.

The equations given in the question are,
$x+y=3$ and $x-y+3=0$
They can be rewritten as,
$x+y=3$ and $x-y=-3$
Also, it is given that the diagonals intersect at $(2,4)$. Draw the parallelogram representing the given data as shown below,

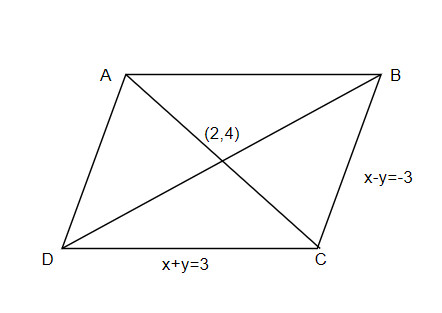
AThe vertex C is a point that intersects the lines DC and BC. Therefore, the coordinates of the C can be obtained by adding and solving the two equations of the lines as below,

& x+y=3 \\\ & x-y=-3 \\\ \end{aligned}}{\begin{aligned} & 2x=0 \\\ & x=0 \\\ \end{aligned}}$$ Substituting the value of $$x$$, we have the value of $$y$$ as, $$\begin{aligned} & 0+y=3 \\\ & \Rightarrow y=3 \\\ \end{aligned}$$ Therefore, the coordinates of C are $$(0,3)$$. The coordinates of vertex B can be obtained by supposing $$x=p$$in the equation $$x-y=-3$$. So, we have the coordinates as $$(p,3+p)$$. To get the coordinates of vertex D, suppose $$x=q$$in the equation $$x+y=3$$. So, we have the coordinates as $$(q,3-q)$$. Let the coordinates of vertex A be $$(m,n)$$. The figure can be redrawn with the above details as below, 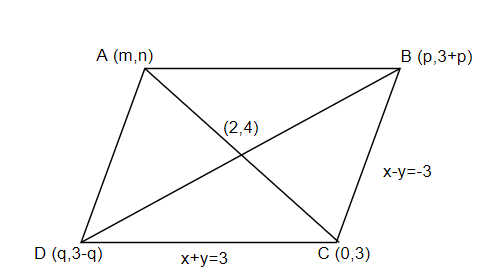 The coordinates of the point of intersection of the diagonals are given as $$(2,4)$$. The point of intersection is the midpoint of the line AC as well as the line BD. It divides the lines in the ratio $$1:1$$. Using the section formula, the coordinates of vertex A $$(m,n)$$ can be found as, $$\left( \dfrac{m+0}{2},\dfrac{n+3}{2} \right)=\left( 2,4 \right)$$ Equating both coordinates on either sides, $$\begin{aligned} & \dfrac{m}{2}=2,\dfrac{n+3}{2}=4 \\\ & m=4,n=(8-3) \\\ & m=4,n=5 \\\ \end{aligned}$$ Therefore, coordinates of A are $$(4,5)$$. Using section formula to find the coordinates of D and B, $$\begin{aligned} & \left( \dfrac{p+q}{2},\dfrac{3+p+3-q}{2} \right)=(2,4) \\\ & \left( \dfrac{p+q}{2},\dfrac{p-q+6}{2} \right)=(2,4) \\\ \end{aligned}$$ Equating both coordinates on either sides, $$\begin{aligned} & p+q=4,p-q=(8-6) \\\ & p+q=4,p-q=2 \\\ \end{aligned}$$ We get two equations $$p+q=4$$ and $$p-q=2$$. Adding and solving the two equations, $$\dfrac{\begin{aligned} & p+q=4 \\\ & p-q=2 \\\ \end{aligned}}{\begin{aligned} & 2p=6 \\\ & p=3 \\\ \end{aligned}}$$ Substituting the value of $$p$$, we have the value of $$q$$ as, $$\begin{aligned} & 3+q=4 \\\ & q=1 \\\ \end{aligned}$$ Now, re-substituting these values, we can get the coordinates of B and D as, B$$(p,3+p)\Rightarrow (3,3+3)=(3,6)$$ D$$(q,3-q)\Rightarrow (1,3-1)=(1,2)$$ Looking at the options, the only possible answer is the coordinates of B, which is $$(3,6)$$. Therefore, we get option (d) as the correct answer. Note: One way in which this problem could go wrong is by interchanging the coordinates of B and D which are written in terms of $$p$$ and $$q$$. If you write the coordinates as $$(3+p,p)$$ and $$(3-q,q)$$ instead of $$(p,3+p)$$and $$(q,3-q)$$, you might end up getting the coordinates as $$(6,3)$$ and $$(2,1)$$ and choose the wrong option.