Question

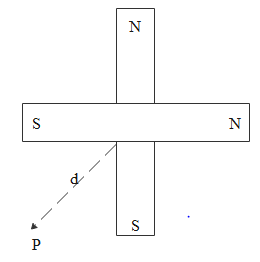
Two short magnets of equal dipole moments M are fastened perpendicularly at their centres as given in the figure. The magnitude of the magnetic field at a distance d from the centre on the bisector of the right angle is

A. $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$
B. $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{M\sqrt 2 }}{{{d^3}}}$
C. $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M\sqrt 2 }}{{{d^3}}}$
D. $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\sqrt {2M} }}{{{d^2}}}$

Answer 1

For a particular bar magnet we have various expressions to find out the magnetic fields at the axial points and equatorial points. Here in this problem we will find out the resultant magnetic moment along the direction of perpendicular bisector and we find out magnetic field due to that resulting magnetic moment

Formula used:
\eqalign{ & {B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{d^3}}} \cr & {B_{equatorial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}} \cr}

Complete step by step answer:
In case of a short bar magnet of magnetic moment M we have two expressions for finding magnetic intensities at a point which is at a distance d on both axial and equatorial lines.
Incase of a point which is at a distance d on the axial line we have equation for magnetic field intensity as ${B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{d^3}}}$
In case of a point which is at a distance d on the equatorial line we have equation for magnetic field intensity as ${B_{equatorial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$
For the given magnet setup we should find the resultant magnetic moment initially which we get as
${M_{res}} = \sqrt {{M^2} + {M^2}} = \sqrt 2 M$
Now that resultant magnetic moment vector will be in the direction of the perpendicular bisector given.
Hence the point where we are supposed to find out the magnetic intensity has become the axial point for the resultant magnetic moment vector.

So from the axial magnetic field expression we have ${B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2{M_{res}}}}{{{d^3}}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\sqrt 2 M}}{{{d^3}}}$
So the answer would be option C

Note:
The formula which we had used is only valid for the short bar magnets. Short in the sense the distance of the point where we are supposed to find the magnetic field is very much bigger than the length of the bar magnet itself. The other way we can solve this problem is to resolve the components of magnetic moment along the axial and equatorial lines and solve for the magnetic field individually.