Question
Question: Two short electric dipoles are placed as shown. The energy of electric interaction between these dip...
Two short electric dipoles are placed as shown. The energy of electric interaction between these dipoles will be
A.r32kP1P2cosθ
B.r3−2kP1P2cosθ
C.r3−2kP1P2sinθ
D.r3−4kP1P2cosθ
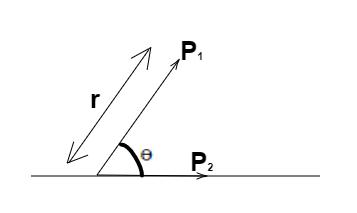
Solution
We are given two short electric dipoles which are inclined at an angle θ with each other. They have some potential energy due to their mutual interaction. We shall therefore apply the basic formula of potential energy of the dipoles but while substituting the values, we must take care of the orientation of the two dipoles with respect to each other.
Complete answer:
The potential energy of interaction of dipoles, U is expressed as:
U=−r32kP1P2
Where,
k=4πε01 and ε0=8.85×10−12Fm−1 and is called the permittivity of free space
⇒k=9×109
P1= dipole moment of one dipole
P2= dipole moment of second dipole
r= distance between the dipole and the position vector
Here, those component dipole moments must be taken which is parallel to the position vector of the dipole.

The vertical component of dipole P1 becomes equal to zero and the horizontal component is considered further. Therefore, we shall the dipole moments as P1cosθ and P2 because the two dipoles are inclined at angle θwith each other.
Thus, substituting the values, we get
U=−r32kP1cosθP2
⇒U=−r32kP1P2cosθ
Hence, the energy of electric interaction between these dipoles is −r32kP1P2cosθ.
Therefore, the correct option is (B) −r32kP1P2cosθ.
Note:
Every dipole has its own electric potential which is given by r2kPcosθ where the symbols have their usual meaning. However, the dipole does not have any potential energy when it is isolated. It develops a potential energy only when another dipole comes in its vicinity and interacts with it. In that case, both the dipoles develop their own potential energy due to their mutual interaction.
