Question

Two short bar magnets of magnetic moments ‘$M$’ each are arranged at opposite corners of a square of side ‘$d$’ such that their centers coincide with the corners and their axes are parallel to one of the sides of the square. If the like poles are in the same direction, the magnetic induction at any of the other corners of the square is?
A. $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$
B. $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{d^3}}}$
C. $\dfrac{{{\mu _0}}}{{2\pi }}\dfrac{M}{{{d^3}}}$
D. $\dfrac{{{\mu _0}}}{{2\pi }}\dfrac{{2M}}{{{d^3}}}$

Answer 1

The direction of the magnetic field of the two bar magnets as well as its magnitudes are determined. To find the direction, the concept that the magnetic field lines always travel from North to South direction is used. The net magnetic field due to both magnets at the point considered is calculated. The formulae for the magnetic field due to a bar magnet at axial and equatorial points are applied in-order to determine the magnetic induction produced due to these magnets on the other points.

Formula used:
The magnetic field intensity at a point placed axially to a short bar magnet is given by:
${\vec B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2m}}{{{d^3}}}$
The magnetic field intensity at a point placed equatorially or perpendicular to a short bar magnet is given by:
${\vec B_{equitorial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{d^3}}}$
Where, $m$ is the magnetic moment and $\dfrac{{{\mu _0}}}{{4\pi }}$ is a proportionality constant.

Complete step by step answer:
The diagram below illustrates a visualization of how the magnets are placed in the opposite corners of a square of side ‘$d$’.

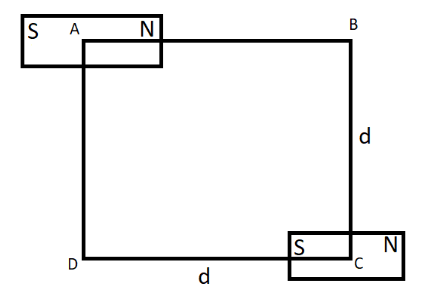
The aim of the problem is to find the magnetic field induced at any one of the other two points where the bar magnets are not placed which means that the magnetic induction at either point B or point D must be calculated. The point we are taking into consideration here is point D. In-order to find this we first need to know the amount of magnetic field induced due to the magnet placed at point C and the magnet placed at point A.

By the properties of magnets we know that magnetic lines flow from the North Pole towards the South Pole forming circular loops. This induces a magnetic moment at point D and the strength or the intensity of this induced magnetic field must hence be calculated.
Let us first consider the magnetic field due to the magnet at point C. We can see that this magnet is placed axially, that is, in the same axis of the point we have considered which is point D. There is an equation for the magnetic field intensity at a point on the axis of a bar magnet. This equation is as follows:
${\vec B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2mr}}{{{{\left( {{r^2} - {l^2}} \right)}^2}}}$
Where, $r$ is the distance between the point and the center of the magnet and $l$ is the length of the magnet.

An important point to note is that it is given in the question that the magnets used are short bar magnets which means the length of the bar magnet is neglected as it is very small in comparison to the $r$ value.
$\Rightarrow {\vec B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2mr}}{{{{({r^2})}^2}}}$
$\Rightarrow {\vec B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2mr}}{{{r^4}}}$
Hence, after cancelling out the common terms the formula becomes:
${\vec B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2m}}{{{r^3}}}$
Here the distance between the point and center of the magnet is given to be $d$. Hence we construct the equation (considering only its magnitude):
${B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2m}}{{{d^3}}}$ -----($1$)
Since the magnetic field is a vector quantity it has both magnitude and direction. We now come to the direction of the magnetic field. We know by the basic property of magnets that like poles repel and unlike poles attract. We consider point D to be a unit north pole and hence the direction will be inwards, that is, along $\overrightarrow {DC}$.

The magnet at point A is placed equatorially from point D. This is shown in the diagram below.

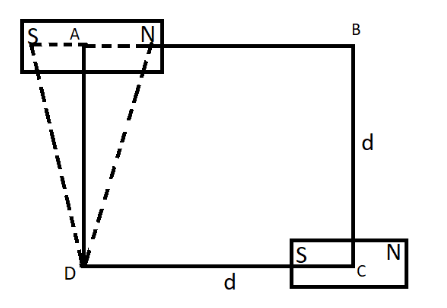
We construct a similar equation for the magnetic field at point D due to magnet A which is at an equatorial point with respect to point D. There is an equation for the magnetic field intensity at a point on the equatorial line of axis of a bar magnet. This equation is as follows:
${\vec B_{equitorial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{{\left( {{r^2} + {l^2}} \right)}^{\dfrac{3}{2}}}}}$
The equation for a short bar magnet by neglecting length will be:
${\vec B_{equitorial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{{\left( {{r^2}} \right)}^{\dfrac{3}{2}}}}}$
$\Rightarrow {\vec B_{equitorial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{r^3}}}$
After substituting $d$ in place of $r$ (considering only its magnitude):
${B_{equitorial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{d^3}}}$ ------($2$)
The direction will be outwards along $\overrightarrow {CD}$ by the property of magnets. The direction vectors from the point D is given by the below diagram.

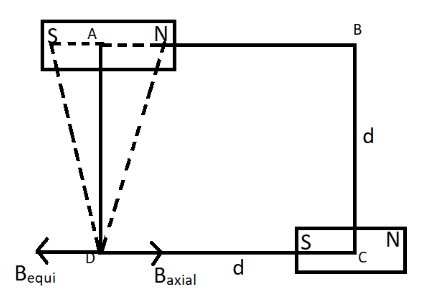
Next, we must calculate the net field intensity at point D. It can be clearly seen that the direction of magnetic field to each of these bar magnets are opposite to each other. Hence the net value will be obtained by taking the difference between them. The magnetic field due to the axial point is more in magnitude and hence the magnetic field due to the equatorial point is subtracted from it. This is given by the equation:
${B_{net}} = {B_{axial}} - {B_{equitorial}}$ ------($3$)

The equations of magnetic field due to axial point and due to equatorial point are substituted in the above equation. By putting equations ($1$) and ($2$) in ($3$) we get (putting M in place of m):
${B_{net}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{d^3}}} - \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$
The common terms are taken out and we get:
${B_{net}} = \dfrac{{{\mu _0}}}{{4\pi {d^3}}}\left[ {2M - M} \right]$
$\Rightarrow {\vec B_{net}} = \dfrac{{{\mu _0}M}}{{4\pi {d^3}}}$ along $\overrightarrow {DC}$
Hence, we obtain the net or the total magnetic field experienced by point D due to the two bar magnets. The direction of this net magnetic field is in the direction of the magnet placed axially to point D because it is greater in magnitude. Therefore, the magnetic induction at the corner D of the square is $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$.

Hence, the correct option is option A.

Additional information: Magnetic lines of force are said to be the curve of the tangent to which at any point gives the direction of the magnetic field at that point. It may also be defined as the path along which a unit north pole will travel if free to do so. These field lines do not really exist but they are useful in representing a magnetic field visually.The lines of force never cross each other because if they do so there will be a possibility of two directions at a single point which would be invalid. The relative closeness of the lines of force gives a measure of the strength of the magnetic field which is maximum at the poles.

Note: Another alternative method to determine the direction of each of the magnetic fields is by using the basic properties of magnets. The magnetic field lines of the magnet placed axially to point D go from north to south and form loops which means the direction of these lines are inwards pointing towards the south pole and hence direction is along $\overrightarrow {DC}$. The magnetic field lines of a magnet at A follow the same property (from north to south pole) and the direction of these lines are outwards along $\overrightarrow {CD}$.