Question
Question: Two ships are \(10km\) apart on a line from south to north. The one farther north is moving towards ...
Two ships are 10km apart on a line from south to north. The one farther north is moving towards the west at 40 kmph and the other is moving towards the north at 40 kmph . Then distance of their closest approach is
A)10km
B)102 km
C)210 km
D)20 km
Solution
Analyze the movement of both the ships using the concepts of relative motion. Draw the respective diagrams describing the motion of ship A with respect to Ship B. Trace the position of both the ships at a time t=t0 and find the shortest distance using the concepts of vector and simple trigonometry.
Complete answer:
As we know from our intuition of kinematics that the distance between two moving points A and B is alternating either in magnitude or direction or both, each point is said to possess a velocity related to another.
Let’s understand the concept in a more practical fashion,
Suppose that B is reduced to rest then the velocity of A relative to B is the velocity with which A will appear to move towards B.
Let’s club it with the scenario which is provided to us in the given question and try doing some diagrammatic analysis.
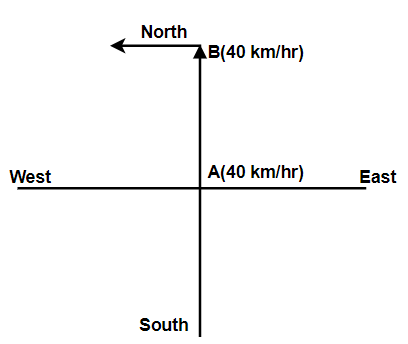
As fig.1 explains that ship A is moving towards North with 40km/hr and ship B is moving towards west with 40km/hr .
Drawing vector diagram for the current scenario will look like :

Velocity of A with respect to B = VAB = VAG−VBG
VAB =40j^−40i^
Magnitude of VAB = 402+402+2×40×40×cos90∘
VAB = 402+402
VAB = 402 (using resultant of vectors, since angle between unit vectors is 90∘
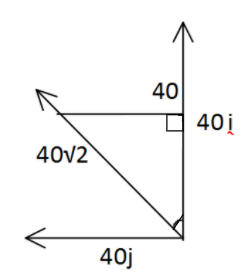
tanθ=4040=1 θ=tan−11=45∘
As B is considered to be at rest, then A is moving towards B with the velocity 40 kmph and an angle of 45∘ with respect to it. As stated in the question, the distance between A and B is 10km . The distance of closest approach is the perpendicular distance between A and B.
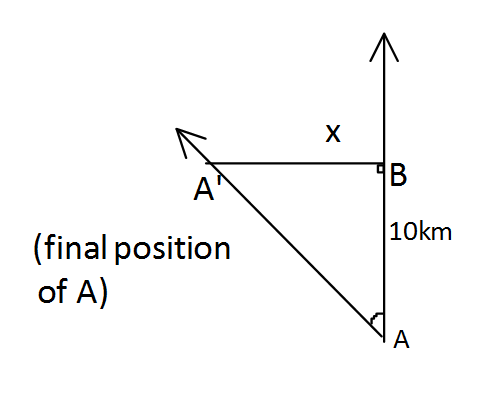
sin∠A′AB=10x 21=10x x=210cm
Note:
To combat such types of problems one needs to trace the motion at different instances and systematically proceed with the concepts of relative motion. Always remember that signs play a crucial role in such problems. Therefore, be very careful with the mathematical operators. Proceed with the concepts of simple kinematics, vector and relative motion and the new layers would automatically start getting unfolded.
