Question

Two ships A and B are sailing straight away from a fixed point O along routes such that, $\angle AOB = {120^o}$. At a certain distance, OA = 8km, OB = 6km and the ship A is sailing at the rate of 20 km/hr. while the ship B sailed at the rate of 30 km/hr. then the distance between A and B is changing at the rate (in km/hr.):
$\left( a \right)\dfrac{{260}}{{\sqrt {37} }}$
$\left( b \right)\dfrac{{260}}{{37}}$
$\left( c \right)\dfrac{{80}}{{37}}$
$\left( d \right)\dfrac{{80}}{{\sqrt {37} }}$

Answer 1

In this particular question use the concept of cosine of angle in any triangle which is given as, $\cos \theta = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$ where a and b are the adjacent sides of that angle and c is the opposite side of that angle and later on differentiate this equation after simplifying w.r.t time so use these concepts to reach the solution of the question.

Complete step by step answer:
Two ships A and B are sailing straight away from a fixed point O along routes such that, $\angle AOB = {120^o}$.

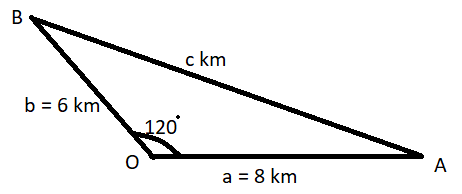
Now it is given that OA = 8 km and OB = 6 km.
Let OA = a, OB = b, and AB = c Km as shown in the following figure.
Now it is also given that A is sailing at the rate of 20 km/hr. while the ship B sailed at the rate of 30 km/hr.
$\Rightarrow \dfrac{{da}}{{dt}} = 20$ Km/hr. and $\dfrac{{db}}{{dt}} = 30$ Km/hr........................ (1)
Now we have to find out the distance between A and B is changing at the rate (in km/hr.) i.e. $\dfrac{{dc}}{{dt}}$
Now apply cosine rule in the above triangle we have,
$\Rightarrow \cos \theta = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$, Where a and b are the adjacent sides of that angle and c is the opposite side of that angle.
$\Rightarrow \cos {120^o} = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
Now as we know that $\cos {120^o} = \dfrac{{ - 1}}{2}$ so we have,
$\Rightarrow - \dfrac{1}{2} = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
$\Rightarrow {a^2} + {b^2} - {c^2} = - ab$
$\Rightarrow {c^2} = {a^2} + {b^2} + ab$................. (2)
Now substitute the values we have,
$\Rightarrow {c^2} = {8^2} + {6^2} + 8\left( 6 \right) = 64 + 36 + 48 = 148$
$\Rightarrow c = \sqrt {148}$................ (3)
Now differentiate equation (2) w.r.t time (t) we have,
$\Rightarrow \dfrac{d}{{dt}}{c^2} = \dfrac{d}{{dt}}{a^2} + \dfrac{d}{{dt}}{b^2} + \dfrac{d}{{dt}}ab$
Now as we know that $\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}},\dfrac{d}{{dx}}mn = m\dfrac{d}{{dx}}n + n\dfrac{d}{{dx}}m$ so we have,
$\Rightarrow 2c\dfrac{{dc}}{{dt}} = 2a\dfrac{{da}}{{dt}} + 2b\dfrac{{db}}{{dt}} + a\dfrac{{db}}{{dt}} + b\dfrac{{da}}{{dt}}$
Now substitute all the values in the above equation we have,
$\Rightarrow 2\sqrt {148} \dfrac{{dc}}{{dt}} = 2\left( 8 \right)\left( {20} \right) + 2\left( 6 \right)\left( {30} \right) + 8\left( {30} \right) + 6\left( {20} \right)$
Now simplify this we have,
$\Rightarrow 2\sqrt {148} \dfrac{{dc}}{{dt}} = 1040$
$\Rightarrow \dfrac{{dc}}{{dt}} = \dfrac{{1040}}{{2\sqrt {148} }} = \dfrac{{520}}{{\sqrt {148} }} = \dfrac{{520}}{{2\sqrt {37} }} = \dfrac{{260}}{{\sqrt {37} }}$ Km/hr.
So this is the required answer.
Hence option (a) is the correct answer.

Note:
whenever we face such types of questions the key concept we have to remember is that always recall the basic differentiating properties such as $\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}},\dfrac{d}{{dx}}mn = m\dfrac{d}{{dx}}n + n\dfrac{d}{{dx}}m$ and always recall the cosine rule in any triangle which is stated above, so use these properties as above applied we will get the required answer.