Question
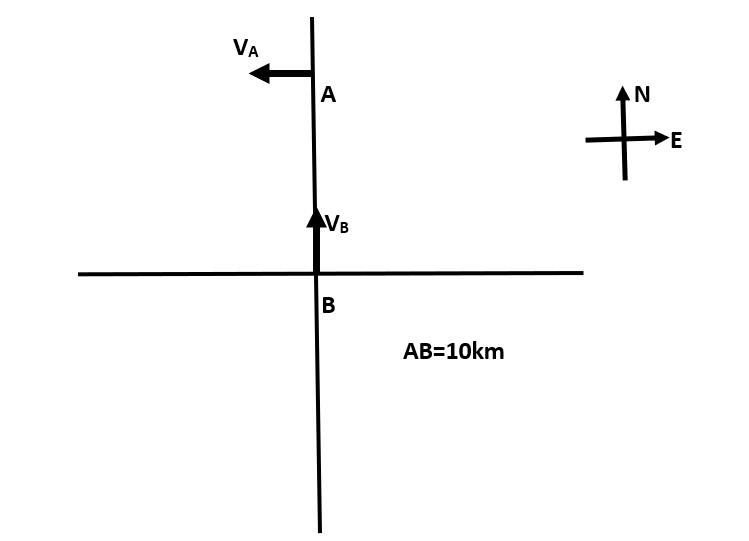
Question: Two ships A and B are 10km apart on a line running South to North. Ship A which is farther North is ...
Two ships A and B are 10km apart on a line running South to North. Ship A which is farther North is streaming West at 20kmhr−1 and Ship B is streaming North at 20kmhr−1 . What is their distance of closest approach and how long do they take to reach it?
Solution
To find the distance of closest approach, we first calculate the relative velocity of one ship with respect to another. This makes one of the ships stationary, so it's easy to move ahead now. Now, from the stationary shop we drop a perpendicular on the line of direction of the moving ship. This perpendicular distance is the minimum distance of approach of the two ships.
Complete answer:
Let us calculate the velocity of ship B with respect to ship A. Then, we have to subtract the velocity of ship A from ship B, as it will relatively at rest with respect to B. Let us understand this by the following figure:
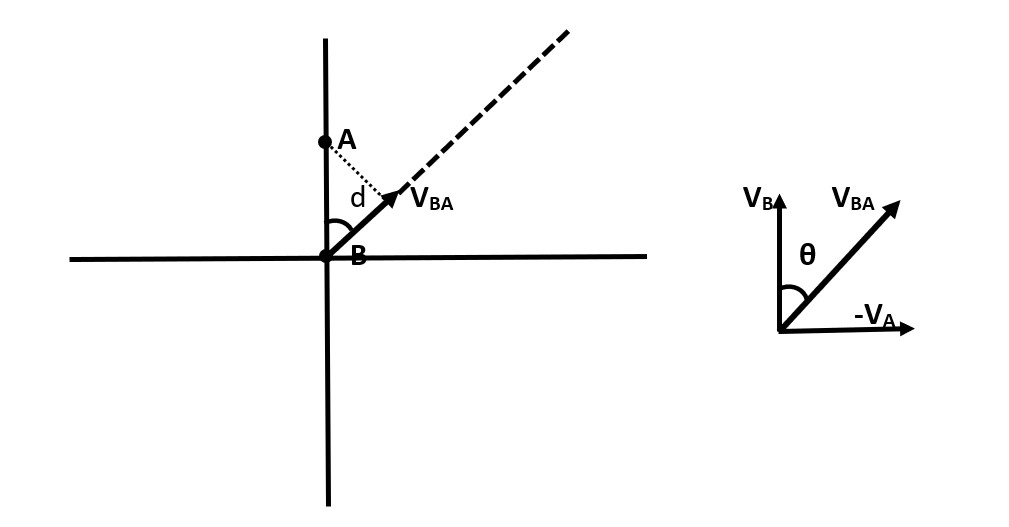
Here, we see the resultant vector VBA making an angle θ with vector VB which is also the angle made by vector VBA with the line joining AB.
Now, since both the vectors are equal in magnitude, therefore the value of angle θ is equal to
=450
Also, the magnitude of vector VBA is equal to:
⇒∣VBA∣=(20)2+(20)2kmhr−1⇒∣VBA∣=202kmhr−1
Now, it has been given in the problem that,
⇒AB=10km
Therefore, the distance of closest approach (say d) will be equal to:
⇒d=ABcos450⇒d=10×21⇒d=52km
Now, let the time taken for traversing this distance be (t) hours. Then, (t) can be calculated using the distance formula as follows:
⇒d=∣VBA∣×t⇒t=∣VBA∣d
Putting the values of all the known terms in the above equation, we get:
⇒t=20252hr⇒t=41hr⇒t=(41×60)min⇒t=15min
Hence, the distance of closest approach comes out to be 52km and the time taken to traverse this distance comes out to be 15 minutes.
Note:
In this problem, if we had used both the velocities in our calculations, then our solution would be larger and calculations would have become more cumbersome. So, it is important to know the approach of different types of questions under different circumstances. It helps us save time and effort and also reduces the chances of error.
