Question

Two rods of same length and material transfer a given amount of heat in $12$ seconds, when they are joined in parallel .But when they are joined in series, then they will transfer same heat in same condition in
A. $24\,s$
B. $3\,s$
C. $1.5\,s$
D. $48\,s$

Answer 1

Use the equation for heat flow through a material between its two ends.According to heat definition, it is one of the essential forms of energy for the survival of life on earth. Transfer of heat takes place from one body to another due to difference in temperature as per thermodynamics.

Formula used:
The equation for heat flow through a material between its two ends is given by,
$Q = \dfrac{{kA\Delta \theta }}{d}t$
where , $k$ is the coefficient of thermal conductivity $A$ is the surface area of the materials through which the heat flows $d$ is the separation between its two surface $\Delta \theta$ is the temperature difference between its two surface and $t$ is the time taken to flow the heat.

Complete step by step answer:

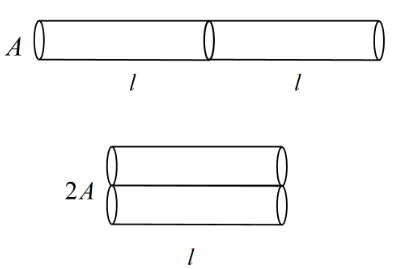
Now, here we have two rods of same length ( say, $l$) and material. Hence, the value of $k$ is the same for both. Let's say the surface area of each rod is $A$. Now, we can say when they are joined parallel the total surface area becomes $A + A = 2A$ but the length remains the same $l$. Total time given to flow is $t = 12$. Hence, putting the values in the equation we get, $Q = \dfrac{{k\left( {2A} \right)\Delta \theta }}{l} \times 12$.

Now, they are joined in series and the same heat $Q$ flows through them. here we have, the surface area remains same i.e. $A$ but the length of the rods become $l + l = 2l$ as they are joined in series. Hence, putting the values in the equation we get, $Q = \dfrac{{kA\Delta \theta }}{{2l}}t$. Therefore, equating the equations we get,
$\dfrac{{k\left( {2A} \right)\Delta \theta }}{l} \times 12 = \dfrac{{kA\Delta \theta }}{{2l}}t$
On simplifying we get,
$2 \times 12 = \dfrac{1}{2}t$
$\therefore t = 48\,s$
Hence, it will take $48\,s$ to flow the same amount of heat through the rods when they are joined in series.

Hence, the correct answer is option (D).

Note: The heat flow through a material is dependent on the temperature differences of the opposite surfaces. Hence, the temperature differences have been kept constant for both the conditions here. If the material was different with given coefficient ${k_1}$ and ${k_2}$ then we could find the heat flow through them as, $Q = \dfrac{{A\Delta \theta }}{{\dfrac{{{d_1}}}{{{k_1}}} + \dfrac{{{d_2}}}{{{k_2}}}}}t$