Question

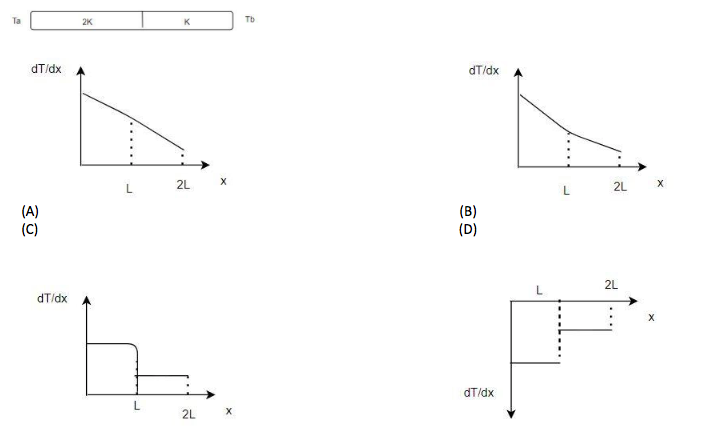
Two rods of same length and cross- sectional area are joined in series. Thermal conductivity of the rods are in the ratio of $2:1$. The ends are maintained at temperature ${\theta _A}$ and ${\theta _B}$ as shown with ${\theta _A} > {\theta _B}$ and sides are thermally insulated. Which of the following graph represents temperature gradient $\left( {\dfrac{{dT}}{{dx}}} \right)$ against $x$ in steady state:

Answer 1

To calculate the temperature gradient of the two rods $A$ and $B$, use the formula of the heat rate flow in the conductor. Substitute the given parameters in the formula and analyze the result obtained to draw the graph of the temperature gradient.

Useful formula:
The thermal current is given by
$dH = \dfrac{{\Delta T}}{{KA}}$
Where $dH$ is the heat rate flow in the conductor, $A$ cross sectional area, $K$ is the thermal conductivity and the $\Delta T$ is the temperature gradient.

Complete step by step solution:
It is given that the
The rods have the same length $l$ and the same cross section $A$.
The ratio of the thermal conductivity of the rods, ${T_1}:{T_2} = 2:1$
The temperature of the first rod is maintained greater than the temperature of the second rod.
Since the rods possess the same length and the area the thermal current on the rod will also be the same. By using the formula of thermal current.
$dH = \dfrac{{\Delta T}}{{KA}}$
Substituting the values,
$dH = \dfrac{{\left( {\dfrac{{dT}}{{dx}}} \right)}}{{2KA}}$

Since the thermal current in the rods is the same, their temperature gradient is negative.
$\dfrac{{dT}}{{dx}} = \dfrac{{ - dH}}{{2KA}}$
Similarly, calculating the temperature gradient for the second rod,
$dH = \dfrac{{\Delta T}}{{KA}}$
$dH = \dfrac{{\left( {\dfrac{{dT}}{{dx}}} \right)}}{{KA}}$
Similarly, the temperature gradient has a negative constant value since the thermal current is the same.
$\dfrac{{dT}}{{dx}} = \dfrac{{ - dH}}{{KA}}$
Hence both the temperature gradient lies below the x axis.

Thus the option (D) is correct.

Note: The main concept in this problem is the negative sign in the temperature gradient between the rods. Since the thermal current or the heat rate flow in the rods are the same, then it has a constant negative temperature gradient.