Question

Two rods of length ${L_2}$​ and coefficient of linear expansion ​ ${\alpha _2}$ are connected freely to a third rod of length ${L_1}$​ of coefficient of linear expansion ${\alpha _1}$​ to form an isosceles triangle. The arrangement is supported on the knife edge at the midpoint of ${L_1}$​ which is horizontal. The apex of the isosceles triangle is to remain at a constant distant from the knife edge if:
$(A)\dfrac{{{L_1}}}{{{L_2}}} = \dfrac{{{\alpha _2}}}{{{\alpha _1}}}$
$(B)\dfrac{{{L_1}}}{{{L_2}}} = \sqrt {\dfrac{{{\alpha _2}}}{{{\alpha _1}}}}$
$(C)\dfrac{{{L_1}}}{{{L_2}}} = 2\dfrac{{{\alpha _2}}}{{{\alpha _1}}}$
$(D)\dfrac{{{L_1}}}{{{L_2}}} = 2\sqrt {\dfrac{{{\alpha _2}}}{{{\alpha _1}}}}$

Answer 1

Firstly we will find a relationship between ${L_1}$ , ${L_2}$ and $d$ with the help of the Pythagoras theorem. Then we will put the condition for the distance $d$ to be constant. In the end, we will apply the formula of linear expansion to get the final answer.

Complete step by step solution:
According to the question, the figure of this question will be,

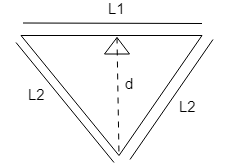
In this question we need to find the value of $d$.
Since, the length $d$ is the midpoint of ${L_2}$, so $d$ acts as a median.
According to properties of a triangle, the median drawn on an isosceles triangle is perpendicular to the base. So, in case of an isosceles triangle the median acts as a perpendicular.
Now, on applying the Pythagoras theorem on the smaller triangle, we get,
$L_2^2 = {d^2} + {\left( {\dfrac{{{L_1}}}{2}} \right)^2}$
${d^2} = L_2^2 - {\left( {\dfrac{{{L_1}}}{2}} \right)^2}$
On taking square root on both the sides, we get,
$d = \sqrt {L_2^2 - {{\left( {\dfrac{{{L_1}}}{2}} \right)}^2}} ......(1)$
Now, we have to find the condition in which the apex of the isosceles triangle remains at a constant distant from the knife edge. So, in simple words $d$ must remain constant.
According to equation (1), for $d$ to remain constant, $L_2^2 - {\left( {\dfrac{{{L_1}}}{2}} \right)^2}$ should also remain constant.
So, the above condition can be written as,
$\dfrac{d}{{dt}}\left( {L_2^2 - {{\left( {\dfrac{{{L_1}}}{2}} \right)}^2}} \right) = 0$
$\dfrac{d}{{dt}}\left( {L_2^2 - \dfrac{{L_1^2}}{4}} \right) = 0$
On differentiation, we get,
$2{L_2}\dfrac{{d{L_2}}}{{dt}} - \dfrac{{{L_1}}}{2}\dfrac{{d{L_1}}}{{dt}} = 0$
By using the formula of linear expansion, we can write the above equation as,
$2{L_2}({L_2}{\alpha _2}) - \dfrac{{{L_1}}}{2}({L_1}{\alpha _1}) = 0$
$2{L_2}({L_2}{\alpha _2}) = \dfrac{{{L_1}}}{2}({L_1}{\alpha _1})$
$2L_2^2{\alpha _2} = \dfrac{{L_1^2{\alpha _1}}}{2}$
On rearranging the terms on both the sides of the above equation,
$4\dfrac{{L_2^2}}{{L_1^2}} = \dfrac{{{\alpha _1}}}{{{\alpha _2}}}$
When we take the square root on both the sides,
$2\dfrac{{{L_2}}}{{{L_1}}} = \sqrt {\dfrac{{{\alpha _1}}}{{{\alpha _2}}}}$
$\dfrac{{{L_2}}}{{{L_1}}} = \dfrac{1}{2}\sqrt {\dfrac{{{\alpha _1}}}{{{\alpha _2}}}}$
Now we will take reciprocal on both the sides,
$\dfrac{{{L_1}}}{{{L_2}}} = 2\sqrt {\dfrac{{{\alpha _2}}}{{{\alpha _1}}}}$
So, the apex of the isosceles triangle is to remain at a constant distant from the knife edge if $\dfrac{{{L_1}}}{{{L_2}}} = 2\sqrt {\dfrac{{{\alpha _2}}}{{{\alpha _1}}}}$
So, the correct answer is $(D)\dfrac{{{L_1}}}{{{L_2}}} = 2\sqrt {\dfrac{{{\alpha _2}}}{{{\alpha _1}}}}$.

Note:
The Coefficient of Linear Thermal Expansion is defined as the property of a material that characterizes the capability of a plastic to expand when a temperature elevation takes place. It is represented by the symbol $\alpha$. It gives us an idea about how much a developed part will remain dimensionally stable under the act of change in temperature.