Question

Two roads cross at right angles at $O$. One person $A$ walking along one of the roads at $3m/s$ sees another person $B$ walking at $4m/s$ along the other road at $O$, when he is $10m$ off. The nearest distance between the two persons is:
A) $10m$
B) $9m$
C) $8m$
D) $7.2m$

Answer 1

It is clear in this question when two paths are at right angles at any one point and we have to find a minimum distance between two points, we can easily apply Pythagoras theorem. If we know about the distance of both persons from origin then we can apply Pythagoras theorem and the hypothesis of the right angle triangle we get will be the minimum distance between two persons.

Formula used:
According to the Pythagoras theorem, "the square of hypotenuse is equal to the sum of the squares of perpendicular and base in the right angle triangle."
A numeral form Pythagoras can be written as
${(hypotenuse)^2}{\text{ }} = {\text{ }}{\left( {perpendicular} \right)^2}{\text{ }} + {\text{ }}{\left( {base} \right)^2}$
$\Rightarrow {(h)^2} = {(p)^2} + {\left( b \right)^2}$
And for finding distance between two points we can apply the simplest distance formula -
$Distance = speed \times time$

Complete step by step solution:
When one person $A$ is walking on the first road. It will see the person on another road which is at the right angle from the first road as the triangle formed between these three points. One is origin and the other two are both persons.

Now consider both persons are at the nearest distance after time $t$. So, firstly we have to find the distance of both persons from origin are ($OA$ and $OB$)

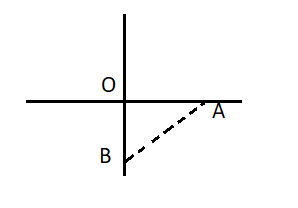
Person $A$ in already $10m$ off so, the distance $OA = {\text{ [}}10 - \left( {speed \times time)} \right]$
According to the question, the speed of a person $A$ is $3m/s$.

$$\Rightarrow OA = 10 - 3t \\\ \Rightarrow OA = (10 - 3t)m \\\$$

The distance between person $B$ and origin.

{ \Rightarrow OB = speed \times time} \\\ { \Rightarrow OB = 4 \times t} \\\ { \Rightarrow OB = 4t m} \end{array}$$ If at time $$t$$, the distance between both persons is nearest then the hypotenuse $$AB$$ will represent the minimum distance. So, according to Pythagoras theorem. $${(AB)^2} = {(OA)^2} + {(OB)^2}$$ Substituting the values of OA and 013.

\Rightarrow {(AB)^2} = {(10 - 3t)^2} + {(4t)^2} \\
\Rightarrow {(AB)^2} = 100 + 9{t^2} - 60t + 100 \\
\Rightarrow {(AB)^2} = 25{t^2} - 60t + 100 \\

Now for making this equation on the polynomial in $$t$$. $$ \Rightarrow {(AB)^2} = 25{t^2} - 60t + 36 + 64$$ $$ \Rightarrow {(AB)^2} = {(5t - 6)^2} + 64$$..................... (i) But we are finding the least distance between both persons. So, by applying $$AB \to min$$ to equation (i) $ \Rightarrow 5t - 6 = 0 \\\ \Rightarrow t = \dfrac{6}{5} \\\ \Rightarrow t = 1.2\sec \\\ $ So, $t = 1.2\sec $ both persons are at the nearest distance from each other. Now, we get from equation (i) $ \Rightarrow [{(5t - 6)^2} + 64] = {(AB)^2}$ Substituting $t = 1.2\sec $ in the above equation.

\Rightarrow [{(5 \times 1.2 - 6)^2} + 64] = {(AB)^2} \\
\Rightarrow {(AB)^2} = [{(6 - 6)^2} + 64] \\
\Rightarrow {(AB)^2} = 64 \\
\Rightarrow AB = 8m \\

Hence, $8m$ is the nearest distance between two persons. **Therefore, option (C) is correct.** **Note:** The nearest distance or least distance between two points is known as displacement. The limit is applied only for the time $$t$$. So, the limit will not be applied on other quantities.