Question

Two rings of the same radius and mass are placed such that their centers are at the common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the center and perpendicular to the plane of one of the ring is (mass of ring = $m$, radius = $r$)
A) $\dfrac{1}{2}m{r^2}$
B) $m{r^2}$
C) $\dfrac{3}{2}m{r^2}$
D) $2m{r^2}$

Answer 1

Inertia of a body is its tendency to resist the change in its shape. The moment of inertia of a rotational system about an axis passing through its center is directly proportional to its mass if the body is moved away from the axis of its rotation. The mass of the system varies with respect to its axis of rotation.

Complete step by step solution:
Step I:
Since the moment of inertia of a rotating system depends on its mass and distribution of mass with respect to its axis of rotation.
Therefore,
Moment of Inertia when the axis is perpendicular to the plane of the ring is given by $= m{r^2}$

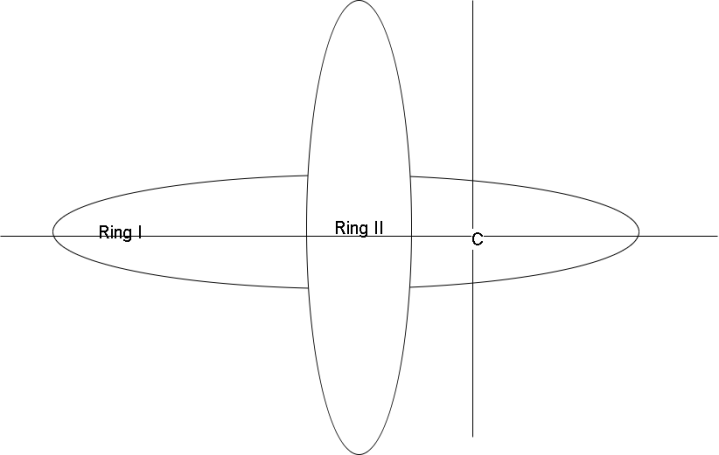
Step II:
Since there are two rings of the same radius and mass, so for the first ring
The moment of inertia when the axis is in-plane to the ring is ${I_1} = m{r^2}$
For the second ring, its axis passes through the center of the first ring and is perpendicular to the plane.
As per perpendicular axis theorem, the center of mass for the perpendicular ring becomes $\dfrac{m}{2}$. Moment of inertia is ${I_2} = \dfrac{{m{r^2}}}{2}$
Step III:
The moment of inertia of the whole system is
$I = {I_1} + {I_2}$
$I = m{r^2} + \dfrac{{m{r^2}}}{2}$
$I = \dfrac{{3m{r^2}}}{2}$

$\therefore$ Moment of inertia of the two rings is $I = \dfrac{3}{2}m{r^2}$. Option (C) is the correct answer.

Note:
Rotational inertia is the inertia is the resistance offered by any system to the change in its rotation. It is a scalar quantity. When distribution of mass in a system changes then rotational motion also changes. Also angular momentum is affected. So basically it is used to calculate angular momentum. Moment of inertia determines the total torque required by the system for its angular acceleration about a rotational axis.