Question

Two resistors of resistance 2R and 3R are connected in series with a battery, which has an emf of E and an internal resistance R. What is the potential difference across the resistor of resistance 2R?

Answer 1

When different resistances are connected to each other in such a way that there is only one direction for electric current to pass, this is referred to as Series Combination. The current flowing through each resistor in a series combination is constant. The potential difference between each resistor in a series combination is different.

Complete step-by-step solution:
In this question, we have been given that there are two resistances having resistance 2R and 3R respectively. These resistances are connected in series combination

But here the battery also has an internal resistance, which has a value of “R”. Internal Resistances are always connected in series with the circuit. Therefore, we can say that we have a total of 3 resistances, of resistance 2R, 3R, and R
Hence, their equivalent resistance will be
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}$
${{R}_{eq}}=2R+3R+R$
${{R}_{eq}}=6R$
Since, we have been given that the emf of battery is “E”, therefore, we can calculate the amount of current as
$I=\dfrac{V}{R}$
$I=\dfrac{E}{{{R}_{eq}}}$
$I=\dfrac{E}{6R}$
Now, according to the question, we need to find out the voltage across the 2R resistor
We know that
$V=IR$
$V=\dfrac{E}{6R}(2R)$
On solving this, we get
$V=\dfrac{E}{3}$

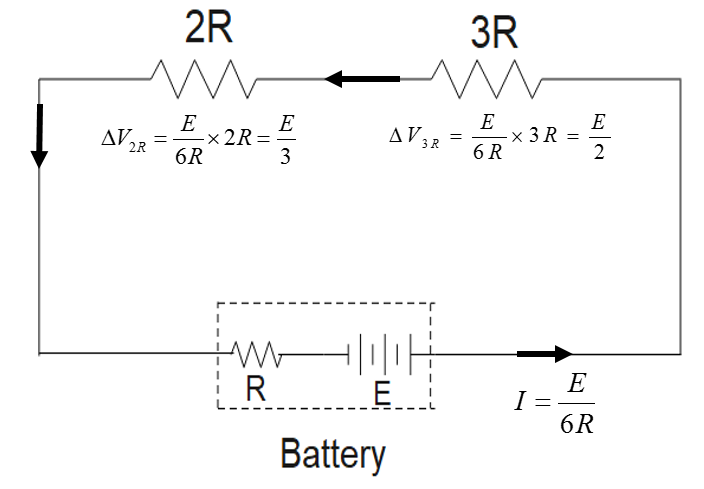
Hence, we can say that the voltage across the 2R resistor will be $V=\dfrac{E}{3}$

Note: When there are several paths for current flow in a circuit, the combination of resistances is referred to as Parallel Combination. The current flowing through each resistor in a parallel combination is different. Each resistor's potential difference is constant. If one component of the circuit (the resistor) is disabled in a parallel combination of resistors, the remaining components of the circuit will continue to function normally.