Question

Two refracting media are separated by a spherical interface as shown in the figure. $PP'$ is the principal axis. ${\mu _1}$ and ${\mu _2}$ are the refractive indices of the medium of incidence and medium of refraction respectively. Then
A. If ${\mu _2} > {\mu _1}$ there cannot be a real image of a real object.
B. If ${\mu _2} > {\mu _1}$ there cannot be a real image of a virtual object.
C. If ${\mu _1} > {\mu _2}$ there cannot be a virtual image of a virtual object.
D. If ${\mu _1} > {\mu _2}$ there cannot be a real image of a real object.

Answer 1

The formula for the refraction in a convex spherical surface is applied in order to determine the relation between the refractive indices, the radius of curvature and the image and object distances. The sign conventions are applied to determine the sign of the image and object distance as well as the radius of curvature. Different cases involving the refractive indices given are applied in order to determine which of the statements of the given options are correct.

Complete step by step answer:
The problem revolves around the concept of refraction of convex spherical surfaces. In order to find out the correct statements we first need to understand the concept behind the refraction of light on a spherical interface.Refraction of light takes place when it is travelling from one medium to another, that is, when there is a difference in the medium it is travelling in.

This means that the refractive indices of the two mediums taken into consideration are also said to be different. In the question, it has been mentioned that ${\mu _1}$ is the refractive index of the medium in which the light is incident. This means that the light travels from medium with refractive index ${\mu _1}$ to the medium of refractive index ${\mu _2}$.

Hence, we have two cases over here that are to be considered. One where the medium with refractive index ${\mu _1}$ is rarer than the medium of refractive index ${\mu _2}$ or a case where the medium with refractive index ${\mu _1}$ is denser than the medium of refractive index ${\mu _2}$.

While considering refraction for spherical interfaces there are certain rules or assumptions which are applied. All distances that are to be measured should be measured from the pole, that is, the center of the spherical interface along the principal axis. All the distances along the direction of the incident light are said to be positive and all the directions along the direction of incident light are said to be taken as negative.

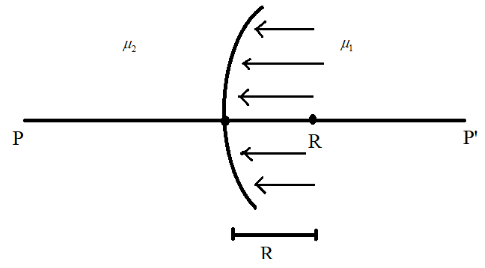
The diagram below illustrates the radius of curvature and the direction of incident of light as per question.

There is an equation relating the radius of curvature of the spherical surface, the image distance and the object distance from the spherical surface. The general formula for light refracting through a spherical interface is given as:
$\dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{R}$ --------($1$)

We now apply sign convention to find the sign for radius of curvature of the spherical interface. This is said to be negative at all times in both of the cases we have considered. This is because the distances against the direction of the incident light is considered as negative and the radius of curvature for the given spherical interface is said to be in the direction opposite to the incident light as shown in the above diagram.

Let us now take the case when the medium with refractive index ${\mu _1}$ is rarer than the medium of refractive index ${\mu _2}$. We are aware that the medium which has a greater refractive index value is said to be denser while the other medium is said to be the rarer medium. By using this concept since we have considered ${\mu _1}$ to be rarer and ${\mu _2}$ to be denser and that light is travelling from rarer to denser medium then we can say that this is the case wherein ${\mu _1} < {\mu _2}$ which can also be written as ${\mu _2} > {\mu _1}$, that is, ${\mu _2}$ is greater than ${\mu _1}$.

We now apply the new sign conventions for spherical interfaces. As we know, there are two possibilities; the object can be either real or virtual. By the rules of sign conventions when the object is said to be real then the object distance, $u$ is said to be taken as negative. The corresponding image that is formed can also be either real or virtual. Similarly, by the rules of sign conventions when the image is said to be real then the image distance, $v$ is said to be taken as positive.

This means that when a real object is considered and when a virtual object is considered then the object distance is said to be negative and positive respectively. Likewise, when a real image is considered and when a virtual image is considered the image distance is said to be positive and negative respectively. This is in accordance with the sign convention given for refraction from spherical interfaces.

Now, we know that the radius of curvature is said to be negative. We apply this on equation ($1$) to get:
$\dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{{ - R}}$
$\Rightarrow \dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{ - ({\mu _2} - {\mu _1})}}{R}$
Hence the signs get reversed and hence the equation becomes:
$\Rightarrow \dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{({\mu _1} - {\mu _2})}}{R}$
Now, by rearranging the terms of equation ($1$) we get:
$\dfrac{{{\mu _2}}}{v} = \dfrac{{{\mu _1} - {\mu _2}}}{R} + \dfrac{{{\mu _1}}}{u}$ --------($2$)

This is done in order to determine the sign of the image distance for the image formed.For the case we have considered, that is, ${\mu _2} > {\mu _1}$, the term $\dfrac{{{\mu _1} - {\mu _2}}}{R}$ will become negative and we consider a real object ($u$ is negative) then the term $\dfrac{{{\mu _2}}}{v}$ will also become negative which means that the sign of $v$ will be negative. This means that the image formed will be a virtual image. This means that for a real object when ${\mu _2} > {\mu _1}$ a virtual image is formed. But however a real image can be formed when a virtual object is considered as per the equation.

Similarly when we consider the case where ${\mu _1} > {\mu _2}$, the term $\dfrac{{{\mu _1} - {\mu _2}}}{R}$ will become positive and we consider a virtual object ($u$ is positive) then the term $\dfrac{{{\mu _2}}}{v}$ will also become positive which means that the sign of $v$ will be positive. This means that the image formed will be a real image. This means that for a virtual object when ${\mu _1} > {\mu _2}$ a real image is formed. But however a virtual image can be formed when a real object is considered as per the equation.

Hence from the conclusions drawn above we can say that for the case ${\mu _2} > {\mu _1}$ there cannot be a real image of a real object and for the case ${\mu _1} > {\mu _2}$ there cannot be a virtual image formed from a virtual object.

Hence, option A and option C are correct.

Note: There may be a confusion in the sign conventions of the distances like the image and object distance and also when the radius of curvature is negative and when it is positive. Even-though the incident rays of the object are said to come from the right side of the spherical surface, usually the object is always taken to be placed at the left side of the spherical surface and hence the object distance is considered to be negative always.