Question
Question: Two rays are incident on a spherical concave mirror of radius R = 5 cm and rays are parallel to prin...
Two rays are incident on a spherical concave mirror of radius R = 5 cm and rays are parallel to principal axis. Choose the correct option (s)
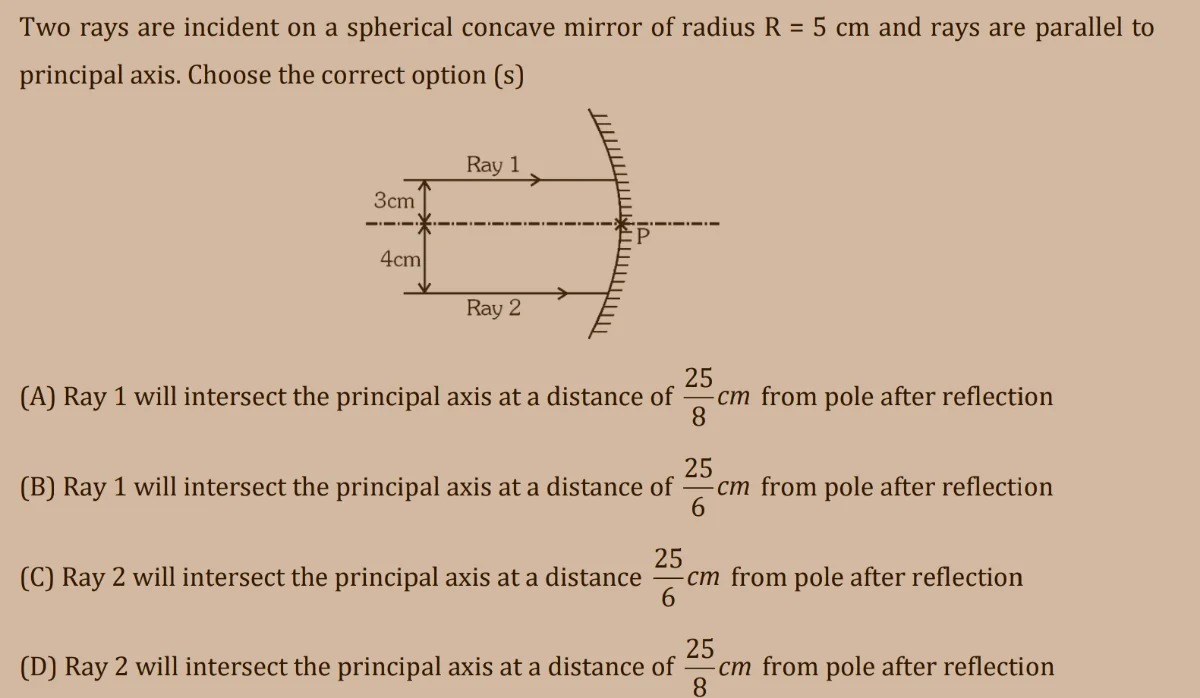
Ray 1 will intersect the principal axis at a distance of 825 cm from pole after reflection
Ray 1 will intersect the principal axis at a distance of 625 cm from pole after reflection
Ray 2 will intersect the principal axis at a distance 625 cm from pole after reflection
Ray 2 will intersect the principal axis at a distance of 825 cm from pole after reflection
Ray 1 will intersect the principal axis at a distance of 825 cm from pole after reflection
Solution
To determine where the reflected rays intersect the principal axis, we can follow these steps:
-
Mirror Placement: Consider the mirror as part of a circle defined by x2+y2=25, with the pole at P=(5,0) and the concave side where x≤5.
-
Incidence Point for Ray 1 (h = 3 cm): The incident point M is calculated as M=(25−9,3)=(4,3).
-
Unit Normal Vector: The unit normal vector n^ at point M is n^=(54,53).
-
Reflected Direction Vector: For an incident ray with direction (−1,0), the reflected direction vr is given by:
vr=vin−2(vin⋅n^)n^=(257,2524).
-
Intersection with Principal Axis: By setting y=0 for the line passing through M with direction vr, the intersection point x is found to be 825 cm from P.
A similar calculation for the second ray (h=−4 cm) will yield a different intersection point, confirming that only ray 1 intersects the axis at 825 cm.
