Question
Question: Two pulleys of radius \(6cm\) and \(10cm\) are connected by a belt. The larger pulley rotates at 40 ...
Two pulleys of radius 6cm and 10cm are connected by a belt. The larger pulley rotates at 40 times per minute. What is the angular velocity (radians per minute) of each pulley?
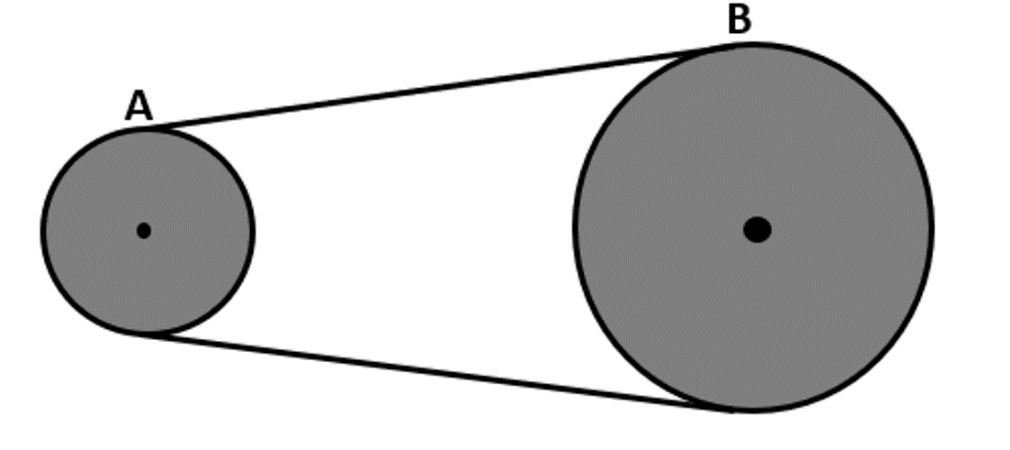
Solution
The rate of revolution of the larger pulley has been provided to us. So, we can use it to easily calculate the angular velocity of the larger pulley. Now, to calculate the angular velocity of the smaller pulley, we use the basic analysis of the system that the speed of the belt at every point will remain constant.
Complete step-by-step solution:
The speed of rotation of the larger pulley is 40 times per minute. By 40 times, it means 40 revolutions per minute. Now we know that one revolution is equal to 2π radian. Then, 40 revolutions per minute will be equal to:
=2π×40
=80π radians per minute
Now, using the value of π as 3.14, we get:
=80×3.14
=251.2 radians per minute
Hence, the angular velocity of the larger pulley comes out to be 251.2 radians per minute.
Now, for the smaller pulley we use the fact that the linear speed of belt is same at all the points. And this linear speed at the contact with the two pulleys is given to be:
For the smaller pulley:
⇒v=r1ω1
Where,
r1 is the radius of the smaller pulley which is equal to 6cm.
ω1 is the angular velocity of the smaller pulley
For the larger pulley:
⇒v=r2ω2
Where,
r2 is the radius of the bigger pulley which is equal to 10cm.
ω2 is the angular velocity of the bigger pulley which is equal to 80π radians per minute.
Thus, equating the linear speed of these two pulleys we get:
⇒6(ω1)=10(80π)⇒ω1=6800×3.14⇒ω1=62512
⇒ω1=418.66 radians per minute.
Hence, the angular velocity of the smaller pulley comes out to be 418.66 radians per minute.
Note: Our analysis of the fact that the linear speed of the belt is the same at every point and is equal to the speed of the pulleys at their circumference is only valid when there is no mention of sliding in the question. That is, there is sufficient friction between the pulley and the belt.
