Question

Two positively charged cylindrical wires of linear charge density ${\lambda _1}$ and ${\lambda _2}$ are placed at distance $+ a$ and $- a$ from mid point. At what distance $x$ will intensity be zero between them

(A) $\dfrac{{\left( {{\lambda _1} + {\lambda _2}} \right)}}{{{\lambda _1} - {\lambda _2}}}a$
(B) $\dfrac{{\left( {{\lambda _1} - {\lambda _2}} \right)}}{{{\lambda _1} + {\lambda _2}}}a$
(C) $\dfrac{{{\lambda _1}a}}{{{\lambda _1} + {\lambda _2}}}$
(D) $\dfrac{{{\lambda _2}a}}{{{\lambda _1} + {\lambda _2}}}$

Answer 1

To solve this question, we need to use the formula for the electric field intensity due to an infinitely long wire of uniform charge density. Then equating the net electric field at the given point to zero, we will get the final answer.

Formula used: The formula used to solve this question is given by
$E = \dfrac{\lambda }{{2\pi {\varepsilon _0}r}}$ , here $E$ is the electric field intensity due to an infinitely long wire of charge density $\lambda$ , at a perpendicular distance $r$ from it.

Complete step by step solution:
Let us consider the point P located at a distance $x$ from the midpoint.

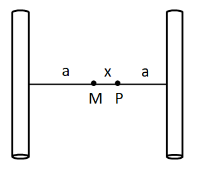
Since the distance of the first wire from the midpoint is equal to $a$ , so the distance of P from the first wire will be equal to $a + x$ . Similarly the distance of P from the second wire is equal to $a - x$ .
$E = \dfrac{\lambda }{{2\pi {\varepsilon _0}r}}$ ……………….(1)
For the first wire, we have $\lambda = {\lambda _1}$ , and $r = a + x$ . Substituting these in (1), we get the electric field due to the first wire at P as
${E_1} = \dfrac{{{\lambda _1}}}{{2\pi {\varepsilon _0}\left( {a + x} \right)}}$ ……………….(2)
For the second wire, we have $\lambda = {\lambda _2}$ and $r = \left( {a - x} \right)$ . Substituting these in (1), we get the electric field due to the second field at P as
${E_2} = \dfrac{{{\lambda _2}}}{{2\pi {\varepsilon _0}\left( {a - x} \right)}}$ ……………….(3)
Now, the net electric field at the point P is
$E = {E_1} - {E_2}$
According to the question, the electric field at P is equal to zero, that is, $E = 0$ . Therefore,
$0 = {E_1} - {E_2}$
$\Rightarrow {E_1} = {E_2}$
From (2) and (3)
$\dfrac{{{\lambda _1}}}{{2\pi {\varepsilon _0}\left( {a + x} \right)}} = \dfrac{{{\lambda _2}}}{{2\pi {\varepsilon _0}\left( {a - x} \right)}}$
Cancelling $2\pi {\varepsilon _0}$ from both the sides, we get
$\dfrac{{{\lambda _1}}}{{\left( {a + x} \right)}} = \dfrac{{{\lambda _2}}}{{\left( {2a - x} \right)}}$
By cross multiplication, we have
${\lambda _1}\left( {a - x} \right) = {\lambda _2}\left( {a + x} \right)$
$\Rightarrow \left( {{\lambda _1} + {\lambda _2}} \right)x = \left( {{\lambda _1} - {\lambda _2}} \right)a$
Dividing both sides by $\left( {{\lambda _1} + {\lambda _2}} \right)$ , we finally get
$x = \dfrac{{\left( {{\lambda _1} - {\lambda _2}} \right)}}{{\left( {{\lambda _1} + {\lambda _2}} \right)}}a$
Therefore, the distance at which the intensity is zero is $\dfrac{{\left( {{\lambda _1} - {\lambda _2}} \right)}}{{\left( {{\lambda _1} + {\lambda _2}} \right)}}a$ .
Hence, the correct answer is option B.

Note:
In this question, no information regarding the length of the wires was given. Therefore we assumed both of them to be infinitely long. Also, the distance $x$ must not be taken from either of the wires. The midpoint is mentioned in the figure given in the question and hence the distance $x$ is taken from it.