Question

Two poles of heights $6m$and $11m$ stand on a plane ground. If the distance between the feet of the poles is $12m$, find the distance between their tops.

Answer 1

Hint- This question can be solved by using Pythagoras theorem.

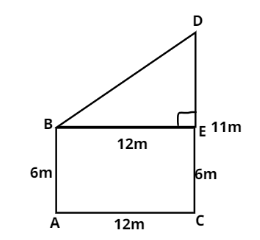
It is given that
Height of the first pole is $AB = 6m$
Height of the second pole is $CD = 11m$
Distance between the feet of poles is $AC = 12m$
We have to find the distance between the tops of pole, i.e. $BD$
Let us draw a line $BE \bot DC$
Since, it is clear from the figure that $AC \bot DC$ as pole is vertical to ground.
So, $BE = AC = 12m$
Similarly, $AB = EC = 6m$
Now,
$DE = DC - EC \\\ DE = 11 - 6 \\\ DE = 5m \\\$
It is clear from the figure that the angle$\angle BED$ , is ${90^ \circ }$ because$BE \bot DC$
Thus, the triangle $BED$ is a right angled triangle.
By using Pythagoras theorem in the right angle triangle.
${\left( {hyp} \right)^2} = {\left( {base} \right)^2} + {\left( {height} \right)^2} \\\ \Rightarrow {\left( {BD} \right)^2} = {5^2} + {12^2} \\\ {\text{or }}{\left( {BD} \right)^2} = 25 + 144 \\\ {\text{or }}{\left( {BD} \right)^2} = 169 \\\ {\text{or }}BD = \sqrt {169} \\\ BD = 13m \\\$
Hence, the distance between the tops of the pole is $13m$.
Note- Whenever we face such types of questions the key concept is that we should draw its figure and then analyze from the figure what we have to find. Like in this question we find the distance between the two poles from their tops by using Pythagoras theorem.