Question
Question: Two poles of height 9m and 14m stand on a plane ground if the distance between their feet is 12m. Fi...
Two poles of height 9m and 14m stand on a plane ground if the distance between their feet is 12m. Find the distance between their tops.
Solution
Hint: First of all draw two poles AB and CD of 9m and 14m respectively and the distance between them that is BD as 12. Now, drop a perpendicular from A to CD and mark the point E. From the figure, find CE by subtracting AB from CD and use Pythagoras theorem in ΔAEC to get the value of AC that is the required value.
Complete step-by-step answer:
In this question, we are given that two poles of height 9m and 14m stand on a plane ground if the distance between their feet is 12m. We have to find the distance between their tops. Let us draw two poles AB and CD of heights 9m and 14m respectively. Also, BD is equal to 12m. Drop a perpendicular from A on CD and name point E.
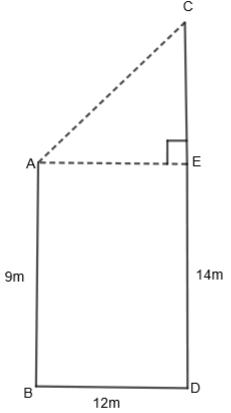
In the above figure, AB = 9m, CD = 14m, BD = 12m, AE⊥CD and we have to find the value of AC. In the above figure, we can write CD as the sum of CE and CD, that is,
CD = CE + ED……(i)
As we know that both towers are parallel to each other. So, we get,
AB = ED
We know that AB = 9m. So, we get,
AB = ED = 9m
By substituting the value of ED in equation (i), we get,
CD = CE + 9m
We know that CD = 14m, so we get,
14m = CE + 9m
CE = 14m – 9m
CE = 5m
From the figure, we can see that AE is parallel to BD. So, we get,
AE = BD
We know that BD = 12m. So, we get AE = BD = 12m.
Now, we know that the Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides. So by using Pythagoras theorem in ΔAEC, right-angled at E, we get,
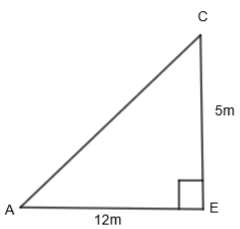
(AE)2+(CE)2=(AC)2
By substituting the value of AE = 12m and CE = 5m, we get,
(12)2+(5)2=(AC)2
144+25=(AC)2
169=(AC)2
AC=169
AC=13m
So, we get the value of AC or the distance between the top of the poles as 13m.
Note: In these types of questions, whenever we are asked to find the distance between two points, we always have to find the straight line distance between those two points. Also, in these questions, students are advised to always draw the diagram to visualize and easily solve the question. And properly substitute the values while using Pythagoras theorem to avoid any mistakes.
