Question

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 meters wide. From a point between them on the road, the angles of elevation of the top of the poles are ${60^0}$ and ${30^0}$, respectively. Find the height of the poles and the distance of the point from the poles.

Answer 1

The angle made between the two points with the horizontal is known to be the angle of depression or the angle of elevation according to the need of the question. We will use here the trigonometric ratios.
Here in the question, we need to determine the distance between the poles and the height of the poles for which we need to use the trigonometric identities as $\tan \theta = \dfrac{{base}}{{height}}$ in the right angle triangle.

Complete step-by-step solution
From the foot of the ground to the top of the poles, the angles of elevation are ${60^0}$ and ${30^0}$, respectively. According to the question, following the rough sketch is drawn

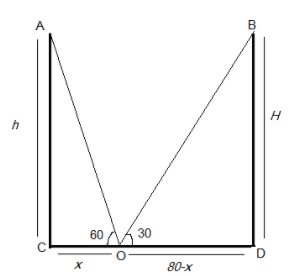
Consider the distance between the first pole and the point on the ground be $x$ then, the distance between another pole and the ground will be $\left( {80 - x} \right)$.
In the triangle ACO, applying the Pythagoras theorem as:
$\tan 60 = \dfrac{{AC}}{{OC}} \\\ \sqrt 3 = \dfrac{h}{x} \\\ h = \sqrt 3 x - - - - (i) \\\$

Again in the triangle BDO, applying the Pythagoras theorem as:
$\Rightarrow \tan 30 = \dfrac{{BD}}{{OD}} \\\ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{H}{{80 - x}} \\\ \Rightarrow 80 - x = H\sqrt 3 - - - - (ii) \\\$
Also, from the question, the height of the poles are equal so, $h = H$
Substitute $h = \sqrt 3 x$ from equation (i) in equation (ii) we get,
$\Rightarrow 80 - x = \left( {\sqrt 3 x} \right)\sqrt 3 \\\ \Rightarrow 80 - x = 3x \\\ \Rightarrow 4x = 80 \\\ \Rightarrow x = 20{\text{ m}} \\\$
Again, substitute $x = 20$ in equation (i) to determine the height of the poles as:

$h = \sqrt 3 x \\\ = 20\sqrt 3 {\text{ m}} \\\$
Hence,
The distance between the point on the ground to the pole 1 is $20{\text{ meters}}$
The distance between the point on the ground to the pole 2 is $80 - 20 = 60{\text{ meters}}$
The height of the poles is $20\sqrt 3 {\text{ meters}}$.

Consider the distance between the first pole and the point on the ground to be $x$ then, the distance between another pole and the ground will be $\left( {80 - x} \right)$.

In the triangle ACO, applying the Pythagoras theorem as

$\tan 60 = \dfrac{{AC}}{{OC}} \\\ \sqrt 3 = \dfrac{h}{x} \\\ h = \sqrt 3 x - - - - (i) \\\$

Again in the triangle BDO, applying the Pythagoras theorem as:

$\tan 30 = \dfrac{{BD}}{{OD}} \\\ \dfrac{1}{{\sqrt 3 }} = \dfrac{H}{{80 - x}} \\\ 80 - x = H\sqrt 3 - - - - (ii) \\\$

Also, from the question, the height of the poles are equal so, $h = H$
Substitute $h = \sqrt 3 x$ from equation (i) in equation (ii) we get,

$\Rightarrow 80 - x = \left( {\sqrt 3 x} \right)\sqrt 3 \\\ \Rightarrow 80 - x = 3x \\\ \Rightarrow 4x = 80 \\\ \Rightarrow x = 20{\text{ m}} \\\$
Again, substitute $x = 20$ in equation (i) to determine the height of the poles as:
$\Rightarrow h = \sqrt 3 x \\\ = 20\sqrt 3 {\text{ m}} \\\$

Hence,
The distance between the point on the ground to the pole 1 is $20{\text{ meters}}$
The distance between the point on the ground to the pole 2 is $80 - 20 = 60{\text{ meters}}$
The height of the poles is $20\sqrt 3 {\text{ meters}}$.

VConsider the distance between the first pole and the point on the ground be $x$ then, the distance between another pole and the ground will be $\left( {80 - x} \right)$.

In the triangle ACO, applying the Pythagoras theorem as:
$\tan 60 = \dfrac{{AC}}{{OC}} \\\ \sqrt 3 = \dfrac{h}{x} \\\ h = \sqrt 3 x - - - - (i) \\\$

Again in the triangle BDO, applying the Pythagoras theorem as:

$\tan 30 = \dfrac{{BD}}{{OD}} \\\ \dfrac{1}{{\sqrt 3 }} = \dfrac{H}{{80 - x}} \\\ 80 - x = H\sqrt 3 - - - - (ii) \\\$

Also, from the question, the height of the poles are equal so, $h = H$
Substitute $h = \sqrt 3 x$ from equation (i) in equation (ii) we get,
$\Rightarrow 8 - x = \left( {\sqrt 3 x} \right)\sqrt 3 \\\ \Rightarrow 80 - x = 3x \\\ \Rightarrow 4x = 80 \\\ x = 20{\text{ m}} \\\$
Again, substitute $x = 20$ in equation (i) to determine the height of the poles as:
$h = \sqrt 3 x \\\ = 20\sqrt 3 {\text{ m}} \\\$
Hence,
The distance between the point on the ground to the pole 1 is $20{\text{ meters}}$
The distance between the point on the ground to the pole 2 is $80 - 20 = 60{\text{ meters}}$
The height of the poles is $20\sqrt 3 {\text{ meters}}$.

Note: In these types of height and distance problems, we should first draw the figure. Then as per requirement, we will choose the angle and relate it with the trigonometric ratio. Find the correlation between the known values and unknown values asked. Remember the general formula about the opposite side, adjacent and hypotenuse properties for all the trigonometric functions along with the trigonometric table for the reference values.