Question

Two poles of equal height are standing opposite to each other on either side of the road which is $80m$ wide. From a point between them on the road, the angles of elevations of the top of the poles are ${{60}^{o}}$ and ${{30}^{o}}$ respectively. Find the height of the poles and the distance of the point from the poles.

Answer 1

Hint: The given question is related to heights and distances. Try to recall the formulae related to trigonometric ratios and values of trigonometric functions for standard angles.
The following formulae will be used to solve the given problem:
(a) $\tan \theta =\dfrac{opposite\,side}{adjacent\,side}$
(b) $\tan \left( {{30}^{o}} \right)=\dfrac{1}{\sqrt{3}}$
(c) $\tan \left( {{60}^{o}} \right)=\sqrt{3}$

Complete step-by-step answer:
Now, considering the information given in the question, we can draw the following figure for better visualization of the problem:

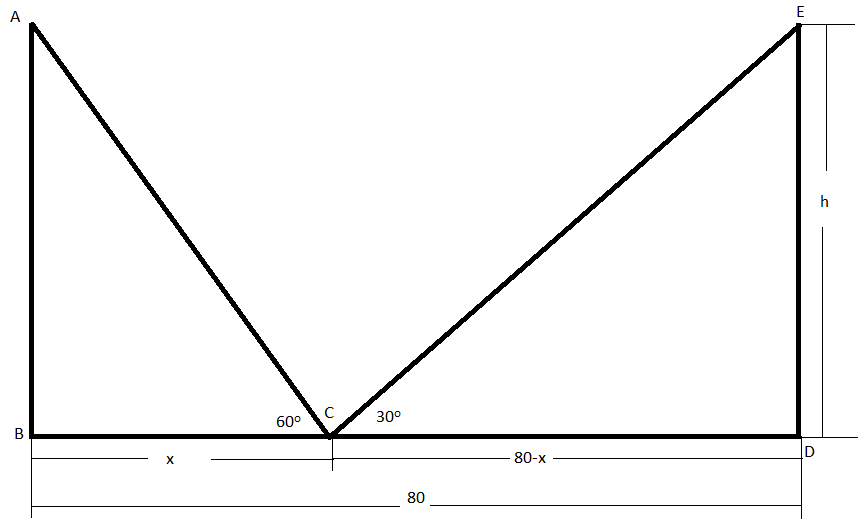
Let $AB$ and $DE$ be the poles of equal height and $BD$ be the road between them. Let the height of the poles be $h$ meter.
In the question, it is given that the width of the road is $80m$ . So, $BD=80$.
We will consider the point $C$ on the line $BD$ such that it is at a distance of $x$ meter from the pole $AB$ . So , the distance of point $C$ from the pole $DE$ will be $(80-x)m$ .
So, $BC=x$ and $CD=80-x$ .
Now, in the question, it is given that the angles of elevation of the top of the poles from point $C$ are ${{60}^{o}}$ and ${{30}^{o}}$.
So, $\measuredangle ACB={{60}^{o}}$ and $\measuredangle ECD={{30}^{o}}$.
Now, we will consider the triangle $\Delta ABC$.
In $\Delta ABC$,
$\tan \left( {{60}^{o}} \right)=\dfrac{h}{x}$
$\Rightarrow \sqrt{3}=\dfrac{h}{x}$
$\Rightarrow h=x\sqrt{3}......(i)$
Now, we will consider the triangle $\Delta ECD$.
In $\Delta ECD$,
$\tan \left( {{30}^{0}} \right)=\dfrac{h}{80-x}$
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{80-x}$
$\Rightarrow h=\dfrac{80-x}{\sqrt{3}}......(ii)$
Now, both heights are equal, i.e. $(i)=(ii)$ .
So, $x\sqrt{3}=\dfrac{80-x}{\sqrt{3}}$
$\Rightarrow 3x=80-x$
$\Rightarrow 3x+x=80$
$\Rightarrow 4x=80$
$\Rightarrow x=20$
So, the distance of the point $C$ from the pole $AB$ is equal to $20m$and hence, the distance of the point$C$ from the pole $DE$ will be equal to $80-x=80-20=60m$.
Now, we need to find the heights of the pole. From equation$(i)$, we have $h=x\sqrt{3}$.
We know, $x=20$. So, $h=20\sqrt{3}m$.
Hence, the distance of the point from the poles is $20m$ and $60m$ and the height of the poles is $20\sqrt{3}m$.

Note: Students are generally confused between the values of $\tan \left( {{30}^{o}} \right)$ and $\tan \left( {{60}^{o}} \right)$. $\tan \left( {{30}^{o}} \right)=\dfrac{1}{\sqrt{3}}$ and $\tan \left( {{60}^{o}} \right)=\sqrt{3}$. These values should be remembered as they are used in various problems of heights and distances.