Question

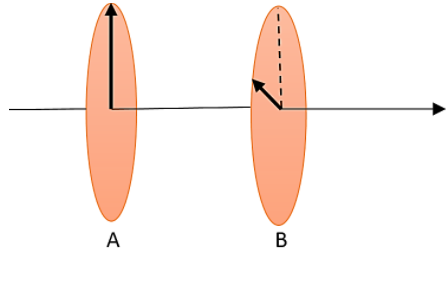
Two Polaroids A and B are placed with their Polaroid axes $30{}^\circ$ to each other as shown in the figure. A plane polarised light passes through the Polaroid A and after passing through it, intensity of light becomes ${{I}_{0}}$​. What will be the intensity of finally transmitted light after passing through the Polaroid B?

& A.0.75{{I}_{0}} \\\ & B.0.866{{I}_{0}} \\\ & A.0.025{{I}_{0}} \\\ & A.0.5{{I}_{0}} \\\ \end{aligned}$$

Answer 1

The intensity $I$ of the transmitted light is changing directly as the square of the cosine of the angle between the analyzer and transmission direction of the polariser. Substitute the angel mentioned in the relation of Malus law.

Formula used:
$I={{I}_{_{0}}}{{\cos }^{2}}\theta$
Where $I$ be the current intensity, ${{I}_{_{0}}}$ be the initial intensity of the light and $\theta$ be the angle between transmission axes and analyzer.

Complete answer:
As we already said, the malus law states that, the intensity $I$ of the transmitted light is changing directly as the square of the cosine of the angle between the analyzer and transmission direction of the polariser.
This can be written in the form of an equation,
$I={{I}_{_{0}}}{{\cos }^{2}}\theta$
As already mentioned in the question, the angle between the transmission axes and the Polaroid is given as
$\theta =30{}^\circ$
Let us substitute this in the equation of malus law,
$I={{I}_{_{0}}}{{\cos }^{2}}30$
As we all know the value of cosine of $30{}^\circ$ is written as,
$\cos 30=\dfrac{\sqrt{3}}{2}$
Taking the square of this,
${{\cos }^{2}}30=0.75$
Substituting this in the equation will give,

& I={{I}_{_{0}}}{{\cos }^{2}}30 \\\ & I={{I}_{_{0}}}\times 0.75 \\\ & I=0.75{{I}_{0}} \\\ \end{aligned}$$ This has been given as the option A. **Therefore the correct answer is option A.** **Note:** When light is incident on a polariser, the transmitted light will get polarised. This polarised beam of light falls on another Polaroid which will transmit light according to the orientation of its axis with the polariser. This is known as analyser. The intensity of light when the light passes through an analyser is given by the Malus law.