Solveeit Logo
Login

Question

Question: Two points O \(\left( 0,0 \right)\) and A \(\left( 3,\sqrt{3} \right)\) along with another point P f...

Two points O (0,0)\left( 0,0 \right) and A (3,3)\left( 3,\sqrt{3} \right) along with another point P form an equilateral triangle. Find the coordinate of P.

Explanation

Solution

Hint: Here we may first calculate the length of one side of the triangle using the given two points then equate it to the length of the sides PA and PO. Since, it’s an equilateral triangle so, the length of all the sides are equal.

Complete step-by-step answer:
Here the two given points are O (0,0)\left( 0,0 \right) and A (3,3)\left( 3,\sqrt{3} \right).
Therefore length of OA can be calculated using length formula which is given as:
According to length formula length between any two points is = (x2−x2)2+(y2−y1)2\sqrt{{{\left( {{x}_{2}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
So, using this formula we have:
OA =(3−0)2+(3−0)2\sqrt{{{\left( 3-0 \right)}^{2}}+{{\left( \sqrt{3}-0 \right)}^{2}}}
= (3)2+(3)2\sqrt{{{\left( 3 \right)}^{2}}+{{\left( \sqrt{3} \right)}^{2}}}
= 9+3\sqrt{9+3}
= 12\sqrt{12}
So, OA = 23  units............(1)2\sqrt{3}\,\,units............(1)
Let us take the coordinates of point P to be (a,b).
Now we may find the length of the sides PA and PO using distance formula.
So, PA = (3−a)2+(3−b)2.............(2)\sqrt{{{\left( 3-a \right)}^{2}}+{{\left( \sqrt{3}-b \right)}^{2}}}.............\left( 2 \right)
Similarly using distance formula to calculate the length of PO, we get:
PO =(0−a)2+(0−b)2\sqrt{{{\left( 0-a \right)}^{2}}+{{\left( 0-b \right)}^{2}}}
Or, PO = a2+b2................(3)\sqrt{{{a}^{2}}+{{b}^{2}}}................(3)
Since, triangle AOP is an equilateral triangle so all the sides are equal i.e. :
OA = PO = PA
First consider the case when:
OA = PO
We may substitute here the lengths of OA and PO from equations (1) and (3) and get:
23=a2+b22\sqrt{3}=\sqrt{{{a}^{2}}+{{b}^{2}}}
On squaring both sides we get:
12=a2+b2............(4)12={{a}^{2}}+{{b}^{2}}............(4)
Now, also we have:
PO = PA
So, again putting values of PO and PA from equations (3) and (2) and squaring both sides we get:
a2+b2=9+a2−6a+3+b2−23b{{a}^{2}}+{{b}^{2}}=9+{{a}^{2}}-6a+3+{{b}^{2}}-2\sqrt{3b}
Or, a2+b2−a2−b2+6a+23b−9−3=0{{a}^{2}}+{{b}^{2}}-{{a}^{2}}-{{b}^{2}}+6a+2\sqrt{3b}-9-3=0
Or, 6a+23b−12=06a+2\sqrt{3}b-12=0
Or, 23b=12−6a2\sqrt{3}b=12-6a
So, from this we can write b as:
b=12−6a23 b =6−3a3.............(5) \begin{aligned} & b=\dfrac{12-6a}{2\sqrt{3}} \\\ & b\,=\dfrac{6-3a}{\sqrt{3}}.............(5) \\\ \end{aligned}
On substituting value of b from equation (5) in equation (4) we get:
12=a2+((6−3a)3)212={{a}^{2}}+{{\left( \tfrac{\left( 6-3a \right)}{\sqrt{3}} \right)}^{2}}
Or, 12=a236+9a2−36a312={{a}^{2}}\dfrac{36+9{{a}^{2}}-36a}{3}
Or, 12×3=12a2−36a+3612\times 3=12{{a}^{2}}-36a+36
Or, 12a(a−6)=012a\left( a-6 \right)=0
From here we can get value of a as:
a=0 or a = 6
On putting a =0 in equation (5) , we get:
b=6−3×03     =63     =23 \begin{aligned} & b=\dfrac{6-3\times 0}{\sqrt{3}} \\\ & \,\,\,\,=\dfrac{6}{\sqrt{3}} \\\ & \,\,\,\,=2\sqrt{3} \\\ \end{aligned}
On putting a = 6 in equation (5) we get:
b=6−3×63     =−123     =−43 \begin{aligned} & b=\dfrac{6-3\times 6}{\sqrt{3}} \\\ & \,\,\,\,=\dfrac{-12}{\sqrt{3}} \\\ & \,\,\,\,=-4\sqrt{3} \\\ \end{aligned}
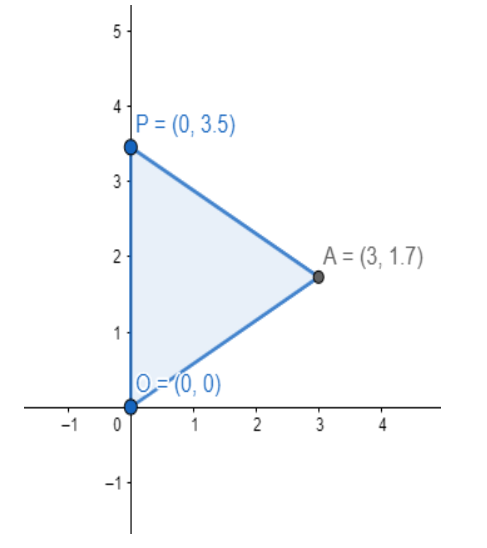
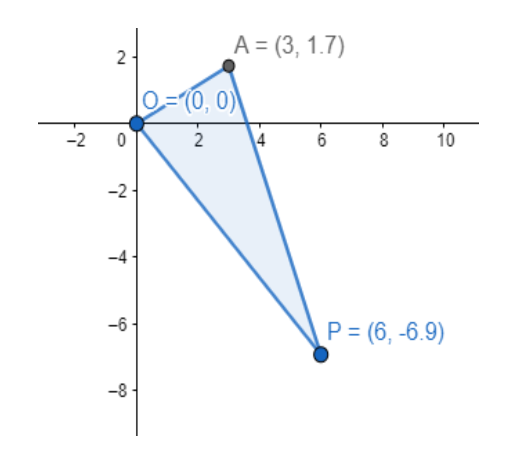
Therefore, the point P can be (0,23)\left( 0,2\sqrt{3} \right) or (6,−43)\left( 6,-4\sqrt{3} \right).


Note: Students should note here that as we obtain a quadratic equation in ‘a’ so, we get two values of a. These two values of a give two values of b correspondingly.